2. Sample Papers
  3. JEE Main & Advanced

JEE Main & Advanced Sample Paper JEE Main Sample Paper-5

  • question_answer
    If the magnitude of tangential and normal accelerations of a particle moving on a curve in a plane be constant throughout, then which of the following represent the variation of radius of curvature with time?

    A)               

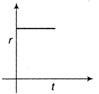
    B)  

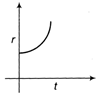
    C)                

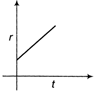
    D)  

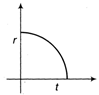
    Correct Answer: B

    Solution :

     Tangential acceleration\[\frac{{{d}^{2}}}{d{{t}^{2}}}={{k}_{1}}\] (constant) \[\Rightarrow \]\[v={{k}_{1}}t+c\] This is a equation for uniform acceleration. Normal acceleration\[\frac{{{v}^{2}}}{r}={{k}_{2}}\] \[\Rightarrow \]\[\frac{{{({{k}_{1}}t+c)}^{2}}}{r}={{k}_{2}}\] \[r=\frac{{{({{k}_{1}}t+c)}^{2}}}{{{k}_{2}}}={{(\alpha t+\beta )}^{2}}\], which is parabola. [Here, r = radius is always positive]


You need to login to perform this action.
You will be redirected in 3 sec spinner