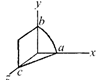
| In given figure, a wire loop has been bent so that it has three segments: segment \[ab\] (a quarter circle), \[bc\] (a square corner), and \[ca\] (straight). Here are three choices for a magnetic field through the loop: |
 |
| (1) \[{{\overset{\to }{\mathop{B}}\,}_{1}}=3\hat{i}+7\hat{j}-5t\hat{k}\] |
| (2) \[{{\overset{\to }{\mathop{B}}\,}_{2}}=5t\hat{i}-4\hat{j}-15\hat{k}\] |
| (3) \[{{\overset{\to }{\mathop{B}}\,}_{3}}=2\hat{i}-5t\hat{j}-1\hat{k}\] |
| Where \[\overset{\to }{\mathop{B}}\,\] is in millitesla and t is in seconds. If the induced current in the loop due to \[{{\overset{\to }{\mathop{B}}\,}_{1,}}{{\overset{\to }{\mathop{B}}\,}_{2}}\] and \[{{\overset{\to }{\mathop{B}}\,}_{3}}\] are \[{{i}_{1,}}\,\,{{i}_{2}}\,\,\text{and}\,\,\,{{i}_{3}}\]respectively then |
A) \[{{i}_{1}}>{{i}_{2}}>{{i}_{3}}\]
B) \[{{i}_{2}}>{{i}_{1}}>{{i}_{3}}\]
C) \[{{i}_{3}}>{{i}_{2}}>{{i}_{1}}\]
D) \[{{i}_{1}}={{i}_{2}}={{i}_{3}}\]
Correct Answer: B
Solution :
| If a \[\ell \]is the side of the square, then area of square, \[{{A}_{1}}={{\ell }^{2}}\] |
| Area of triangle, \[{{A}_{2}}=\frac{{{\ell }^{2}}}{2}\] |
| Area of quarter circle, \[{{A}_{3}}=\frac{\pi {{\ell }^{2}}}{4}\] |
| Total Area of the loop \[\overset{\to }{\mathop{A}}\,={{A}_{1}}\overset{\hat{\ }}{\mathop{i}}\,+{{A}_{2}}\overset{\hat{\ }}{\mathop{j}}\,+{{A}_{3}}\overset{\hat{\ }}{\mathop{k}}\,\]=\[\left( {{\ell }^{2}}\overset{\hat{\ }}{\mathop{i}}\,+\frac{{{\ell }^{2}}}{2}\overset{\hat{\ }}{\mathop{j}}\,+\frac{\pi {{\ell }^{2}}}{4}\overset{\hat{\ }}{\mathop{k}}\, \right)\] |
| Now, \[{{\phi }_{1}}={{\overset{\to }{\mathop{B}}\,}_{1}}.\overset{\to }{\mathop{A}}\,\] \[=(3\overset{\hat{\ }}{\mathop{i}}\,+7\overset{\hat{\ }}{\mathop{j}}\,-5t\overset{\hat{\ }}{\mathop{k}}\,).\left( {{\ell }^{2}}\overset{\hat{\ }}{\mathop{i}}\,+\frac{{{\ell }^{2}}}{2}\overset{\hat{\ }}{\mathop{j}}\,+\frac{\pi {{\ell }^{2}}}{4}\overset{\hat{\ }}{\mathop{k}}\, \right)\] =\[\left( 3{{\ell }^{2}}+\frac{7{{\ell }^{2}}}{2}-\frac{5}{4}\pi {{\ell }^{2}}t \right)\] |
| \[\therefore \left| {{e}_{1}} \right|=\frac{d{{\phi }_{1}}}{dt}=\frac{5}{4}\pi {{\ell }^{2}}\] |
| \[{{\phi }_{2}}={{\overset{\to }{\mathop{B}}\,}_{2}}.\overset{\to }{\mathop{A}}\,\] =\[(5ti-4j-15k).\left( {{\ell }^{2}}\overset{\hat{\ }}{\mathop{i}}\,+\frac{{{\ell }^{2}}}{2}\overset{\hat{\ }}{\mathop{j}}\,+\frac{\pi {{\ell }^{2}}}{4}\overset{\hat{\ }}{\mathop{k}}\, \right)\]=\[\left( 5{{\ell }^{2}}t \right)-2{{\ell }^{2}}-\frac{15\pi }{4}{{\ell }^{2}}\] |
| \[\therefore \left| {{e}_{2}} \right|=\frac{d{{\phi }_{2}}}{dt}=5{{\ell }^{2}}\] |
| \[{{\phi }_{3}}={{\overset{\to }{\mathop{B}}\,}_{3}}.\overset{\to }{\mathop{A}}\,\] =\[\left( 2\overset{\hat{\ }}{\mathop{i}}\,-5t\overset{\hat{\ }}{\mathop{j}}\,-12\overset{\hat{\ }}{\mathop{k}}\, \right).\left( {{\ell }^{2}}\overset{\hat{\ }}{\mathop{i}}\,\frac{{{\ell }^{2}}}{2}\overset{\hat{\ }}{\mathop{j}}\,+\frac{\pi {{\ell }^{2}}}{4}\overset{\hat{\ }}{\mathop{k}}\, \right)\] =\[\left( 2{{\ell }^{2}}-\frac{5}{2}{{\ell }^{2}}t-3\pi {{\ell }^{2}} \right)\] |
| \[\therefore \left| {{e}_{3}} \right|=\frac{5{{\ell }^{2}}}{2}\] |
| Clearly,\[{{e}_{2}}>{{e}_{1}}>{{e}_{3}}\] |
| \[\therefore {{i}_{2}}>{{i}_{1}}>{{i}_{3}}.\] |
You need to login to perform this action.
You will be redirected in
3 sec
