question_answer

The number of integral values of a for which the point \[(a-1,\text{ }a+1)\] lies in the larger segment of the circle \[{{x}^{2}}+{{y}^{2}}-xy6=0\] cut by the chord whose equation is \[x+y-2=0\] is equal to

A) 0

B) 1

C) 2

D) None of these

Correct Answer: B

Solution :

The given circle
\[S(x,y)\equiv {{x}^{2}}+{{y}^{2}}-x-y-6=0\]		? (i)
has centre at\[C\equiv \left( \frac{1}{2},\frac{1}{2} \right)\]
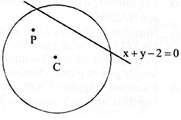According to the required conditions the given point \[P(\alpha -1,\alpha +1)\]Must lie inside the given circle
i.e.\[S(\alpha -1\alpha +1)<0\operatorname{i}.e\] \[\]\[{{(\alpha -1)}^{2}}+{{(\alpha +1)}^{2}}-(\alpha -1)-(\alpha +1)-6<0\]\[\operatorname{i}.e.{{\alpha }^{2}}-\alpha -2<0\]
\[i.e.(\alpha -2)-(\alpha +1)<0\]
\[i.e.-1<\alpha <2\]	? (ii)

And also \[P\]and \[C\]must lie on the same side of the line (see fig.)
\[L(x,y)\equiv x+y-2=0\]		? (iii)
i.e. \[L\left( \frac{1}{2},\frac{1}{2} \right)\] And \[L(\alpha -1,\alpha +1)\]must have the same sign.
Now, since \[L\left( \frac{1}{2},\frac{1}{2} \right)=\frac{1}{2}+\frac{1}{2}-2<0\]
Therefore we have \[L(\alpha -1,\alpha +1)\]\[=(\alpha -1)+(\alpha +1)-2<0\]
i.e. \[\alpha <1\]	?.(iv)
Inequalities (ii) and (iv) together give the permissible values of \[\alpha \]as \[\,-1<\alpha <1\]