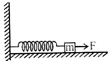
| A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. Trie other end of the spring is fixed, as shown in the figure. The block is initially at rest in its equilibrium position. If now the block is pulled with a constant force F, the maximum speed of the block is: |
 |
A) \[\frac{\pi F}{\sqrt{mk}}\]
B) \[\frac{2\text{F}}{\sqrt{mk}}\]
C) \[\frac{\text{F}}{\sqrt{mk}}\]
D) \[\frac{\text{F}}{\pi \sqrt{mk}}\]
Correct Answer: C
Solution :
| Maximum speed is at mean position (equilibrium). |
| \[\text{F}\,=\,kx,\] \[x\,=\,\frac{\text{F}}{k}\] |
| \[{{\text{W}}_{\text{F}}}+{{\text{W}}_{\text{sp}}}\,=\,\Delta \text{KE}\] |
| \[\text{F}(x)\,-\frac{1}{2}k{{x}^{2}}\,=\,\frac{1}{2}m{{v}^{2}}\,-\,0\] |
| \[\text{F}\left( \frac{\text{F}}{k} \right)\,-\,\frac{1}{2}k{{\left( \frac{\text{F}}{k} \right)}^{2}}=\frac{1}{2}m{{v}^{2}}\] |
| \[\Rightarrow \] \[{{\text{V}}_{\max }}\,=\,\frac{\text{F}}{\sqrt{mk}.}\] |
You need to login to perform this action.
You will be redirected in
3 sec
