A) \[8\,\,(\sqrt{2}-1)\]
B) \[2\,\,(\sqrt{2}+1)\]
C) \[4\,\,(\sqrt{2}+1)\]
D) none of these
Correct Answer: A
Solution :
| Let x be the length of cutted portion than \[2-2x=\sqrt{2}x\] |
| \[x\,\,(2+\sqrt{2})=2\] |
| \[x=\frac{2}{\sqrt{2}\,\,(\sqrt{2}+1)}=\frac{\sqrt{2}}{1}\,\,\times \,\,\left( \sqrt{2}-1 \right)\] |
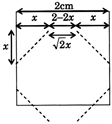 |
| Area of octagon = Area of square - Area of \[4\Delta \] |
| \[=2\times 2-4\,\,\times \,\,\frac{1}{2}.\,\,{{x}^{2}}\]\[=4-\frac{4\,\,\times \,\,1}{2}.{{\left[ \sqrt{2}\,\,(\sqrt{2}-1) \right]}^{2}}\] |
| \[=4-4\,\,{{(\sqrt{2}-1)}^{2}}\]\[=4\,\,\left[ 1-2-1+2\,\sqrt{2} \right]\]\[=8\,\,(\sqrt{2}-1)\] |
You need to login to perform this action.
You will be redirected in
3 sec
