question_answer

.

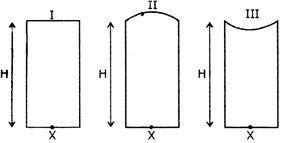
Three glass cylinders of equal height \[H=30cm\] and me refractive index \[n=1.5\] are placed on a horizontal surface as shown in figure. Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same \[(R=3m).\] If \[{{\text{H}}_{\text{1}}}\text{,}\]\[{{\text{H}}_{2}}\] and \[{{\text{H}}_{\text{3}}}\] are the apparent depths of a point X on the bottom of the three cylinder, respectively, the correct statement(s) is/ are:

A) \[{{\text{H}}_{\text{3}}}\,>\,{{\text{H}}_{\text{1}}}\]

B) \[0.8\,\text{cm}\,<\,({{H}_{2}}-{{H}_{1}})\,<\,0.9\,\text{cm}\]

C) \[{{\text{H}}_{\text{2}}}\,\text{}\,{{\text{H}}_{\text{1}}}\]

D)             \[{{\text{H}}_{\text{2}}}\,\text{}\,{{\text{H}}_{\text{3}}}\]

Correct Answer: C , D

Solution :

\[\frac{d'}{d}=\frac{{{n}^{2}}}{{{n}_{1}}}\]

\[\Rightarrow \]   \[\frac{d'}{30}=\frac{1}{\text{3/2}}\]

\[\Rightarrow \]   \[{{d}^{'}}=20\,\text{cm}\]

\[{{n}_{1}}=1\]

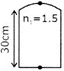\[\frac{1}{v}+\frac{1.5}{30}=\frac{(1-1.5)}{-\,300}\]

\[\Rightarrow \]   \[\frac{1}{v}=+\frac{1}{600}-\frac{3}{60}=\frac{1-30}{600}\]

\[\Rightarrow \]   \[\frac{1}{v}=\,-\,\frac{29}{600}\,\]

\[\Rightarrow \]   \[\frac{1}{v}=\,-\,\frac{600}{29}\,=\,-20.68\,\text{cm}\]

\[{{n}_{1}}=1\]

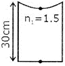\[\frac{1}{v}=\frac{1.5}{-30}=\frac{1-1.5}{300}\]

\[\Rightarrow \]   \[\frac{1}{v}=\frac{-1}{600}-\frac{3}{60}=\frac{-1-30}{600}\,=\,\frac{-\,31}{600}\]

\[\Rightarrow \]   \[v=-\frac{600}{31}=-\,19.35.\]

Solution :

Same as above