A) 0
B) 1
C) 2
D) none
Correct Answer: A
Solution :
| Let \[y=mx+c\] is the variable chord which is subtending right angle at the vertex of parabola hence equation of pair of straight lines OP and OQ can be given by making a homogeneous second degree equation with the help of parabola and chord as follows |
| \[{{y}^{2}}-4ax\left( \frac{y-mx}{c} \right)=0\] |
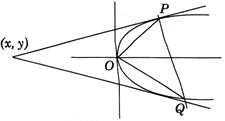 |
| for subtend \[90{}^\circ \] at vertex \[1+\frac{4am}{c}=0\] |
| \[\Rightarrow c=-\,4am\]\[\Rightarrow \]equation of chord is \[y=m\,\,(x-4a)\] |
| Let point of intersection of tangents at the extremeities is \[({{x}_{1}},{{y}_{1}})\] |
| \[y\,{{y}_{1}}=2a(x+{{x}_{1}})\] |
| Which is passing through \[(4a,0)\] |
| \[\Rightarrow {{x}_{1}}+4a=0\]\[\Rightarrow x+4a=0\] is the required locus. |
You need to login to perform this action.
You will be redirected in
3 sec
