| A uniform stick of mass M is placed in a frictionless well as shown. The stick makes angle \[\theta \] was the horizontal. The force which the vertical wall exerts on right end of stick is - |
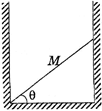 |
A) \[\frac{Mg}{2\cot \theta }\]
B) \[\frac{Mg}{2\tan \theta }\]
C) \[\frac{Mg}{2\cos \theta }\]
D) \[\frac{Mg}{2\sin \theta }\]
Correct Answer: B
Solution :
| The free body diagram of rod is |
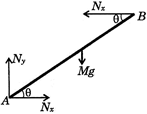 |
| Where \[{{N}_{x}}\] and \[{{N}_{y}}\] are horizontal and vertical components of reaction exerted by wall on rod. Net torque on rod about left end A is zero |
| \[\therefore Mg\frac{\ell }{2}\cos \theta ={{N}_{x}}\ell \sin \theta \]\[\Rightarrow {{N}_{x}}=\frac{Mg}{2\tan \theta }\] |
You need to login to perform this action.
You will be redirected in
3 sec
