| Two magnets A and B are identical and these are arranged as shown. Their lengths are negligible in comparison to separation between them. A magnetic needle is placed between the magnets at point P and it gets deflected through an angle \[\theta .\] The ratio of distances and will be |
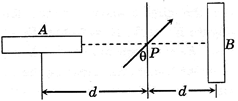 |
A) \[{{(2\cot \theta )}^{1/3}}\]
B) \[{{(2\tan \theta )}^{1/3}}\]
C) \[(2\cot \theta )\]
D) \[{{(2\tan \theta )}^{-1/3}}\]
Correct Answer: A
Solution :
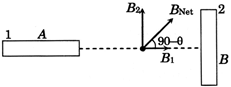 |
| Needle will deflect to magnetic field direction at P |
| At P, B is produced by magnet A and B |
| B due to magnet \[B={{B}_{1}}\] |
| B due to magnet \[A={{B}_{2}}\] |
| Formula of B: At axis of magnet \[A=\frac{{{\mu }_{0}}M}{{{d}^{3}}}\] |
| At equatorial axis of magnet \[B=\frac{2{{\mu }_{0}}M}{{{d}^{3}}}\] |
| \[\therefore {{B}_{2}}=\frac{{{\mu }_{0}}M}{d_{2}^{3}}\] |
| \[{{B}_{1}}=\frac{2{{\mu }_{0}}M}{d_{1}^{3}}\] |
| \[\tan \,\,(90=\theta )=\frac{{{B}_{2}}}{{{B}_{1}}}\] |
| \[\frac{{{B}_{2}}}{{{B}_{1}}}=\cot \theta \] |
| \[\frac{1}{2}{{\left( \frac{{{d}_{1}}}{{{d}_{2}}} \right)}^{3}}=\cot \theta \] |
| \[\frac{d}{{{d}_{2}}}={{(2\cot \theta )}^{1/3}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
