| A square of mass M and sides of length L has a moment of inertia Io when rotated about an axis perpendicular to its surface and passing through its center, as shown. Now a lump of clay, also of mass M is attached to one corner of the square as shown. What is the new moment of inertia of the masses about the same axis of rotation? |
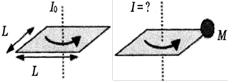 |
A) \[{{I}_{0}}+\frac{M{{L}^{2}}}{4}\]
B) \[{{I}_{0}}+\frac{M{{L}^{2}}}{2}\]
C) \[{{I}_{0}}+\frac{\sqrt{2}M{{L}^{2}}}{2}\]
D) \[{{I}_{0}}+2M{{L}^{2}}\]
Correct Answer: B
Solution :
| The moment of inertia for the system can be calculated by adding the two individual moments of inertia as following |
| \[{{I}_{total}}={{I}_{0}}+{{I}_{clay}}\] |
| \[{{I}_{clay}}=M{{R}^{2}}\] |
| \[R=\sqrt{2}\frac{L}{2}\] |
| \[{{I}_{clay}}=M{{\left( \sqrt{2}\frac{L}{2} \right)}^{2}}=\frac{M{{L}^{2}}}{2}\] |
| \[{{I}_{total}}={{I}_{0}}+\frac{M{{L}^{2}}}{2}\] |
You need to login to perform this action.
You will be redirected in
3 sec
