A) The magnitude of \[{{F}_{3}}\] is the same as that of \[{{F}_{1}}\]
B) The object is in equilibrium and could be stationary
C) \[{{F}_{3}}\] lies in the x-y plane
D) The object is in equilibrium and could be moving
Correct Answer: A
Solution :
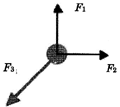
| By definition, the object is in equilibrium, either static (unmoving) or dynamic (moving with a constant velocity). If the object has acceleration a=0, the net force acting on the mass must be 0 as well: |
 |
| \[{{F}_{net}}=ma\] |
| \[{{F}_{net}}=m(0)=0\] |
| With force \[{{F}_{1}}\]and \[{{F}_{2}}\] in the x-y plane, the force that will counteract them must lie in the x-y plane as well, as shown. The magnitude of that force \[{{F}_{3}}\] is equal to the vector sum of \[{{F}_{1}}\] and \[{{F}_{2}}\] and can be calculated as follows: |
| \[\sum{{{F}_{x}}}=0={{\vec{F}}_{2}}-{{\vec{F}}_{3-x}}\] |
| \[\sum{{{F}_{y}}}=0={{\vec{F}}_{1}}-{{\vec{F}}_{3-x}}\] |
| \[\left| \,{{F}_{3}} \right|=\sqrt{F_{3-x}^{2}+F_{3-y}^{2}}\]\[=\sqrt{F_{1}^{2}+F_{2}^{2}}={{F}_{1}}\sqrt{2}\] |
| both graphically and analytically, we can see that the magnitude of \[{{F}_{3}}\] is not the same as that of \[{{F}_{1}}.\] |
You need to login to perform this action.
You will be redirected in
3 sec
