A) 1.9 cm
B) 1.93 cm
C) 1.95 cm
D) 1.98 cm
Correct Answer: C
Solution :
| Mass of the cube = 30g, density of water=\[\rho =1gm/c{{m}^{3}},\] surface tension of water \[=\sigma =70\,\,dyne/cm\] |
| a = length of each face of the cube = 4 cm, let y be the distance of the lower face of the cube from the surface of water. |
| When the cube floats freely in water F (force due to surface tension) |
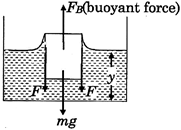 |
| Upward forces = downward force |
| \[{{F}_{B}}={{a}^{2}}y\rho g\] |
| \[F=4a\sigma \] |
| \[{{F}_{B}}=F+mg\] |
| \[{{a}^{2}}y\rho g=4a\sigma +mg\] |
| \[\therefore y=\frac{mg+4a\sigma }{{{a}^{2}}\rho g}=\frac{30\,\,\times \,\,980+4\,\,\times \,\,4\,\,\times \,\,70}{4\,\,\times \,\,4\,\,\times \,\,1\,\,\times \,\,980}\]\[=\frac{29400+1120}{15680}=\frac{30520}{15680}=1.95\,\,cm\] |
You need to login to perform this action.
You will be redirected in
3 sec
