s Sample papers for KVPY KVPY Stream-SX Model Paper-21 - Studyadda.com
  2. Sample Papers
  3. KVPY

KVPY Sample Paper KVPY Stream-SX Model Paper-21

  • question_answer
    An aeroplane is flying in a horizontal circle at a speed of 540 km/h. Banked for this turn, the wings of the plane are tilted at an angle \[45{}^\circ \] from the horizontal. Assume that a lift force acting perpendicular to the wings holds the aircraft in the sky. The radius of the circle in which the plane is flying is \[(Take\,\,\,g=10m/{{s}^{2}})\]

    A) 1000 m

    B) 2250 m

    C) 500 m

    D) 4500 m

    Correct Answer: B

    Solution :

    in vertical direction aeroplane is in equilibrium
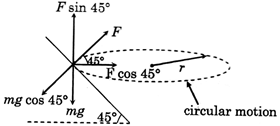    \[\therefore F\sin 45{}^\circ =mg\]
    \[F=\frac{mg}{\sin 45{}^\circ }\]
    Lift force \[F=\frac{mg}{\sin 45{}^\circ }\]
    The centripetal force is provided by the component of lift force
    \[\Rightarrow F\cos 45{}^\circ =\frac{m{{v}^{2}}}{r}\]\[\Rightarrow \frac{mg}{\sin 45{}^\circ }\cos 45{}^\circ =\frac{m{{v}^{2}}}{r}\]
    \[r=\frac{m{{v}^{2}}}{mg}=\frac{{{v}^{2}}}{g}=\frac{{{\left( 540\times \frac{5}{18} \right)}^{2}}}{10}=2250\,\,m\]


You need to login to perform this action.
You will be redirected in 3 sec spinner