| The oscillations represented by curve 1 in the graph are expressed by equation \[x\text{ }=\text{ }A\text{ }sin\omega t.\]The equation for the oscillations represented by curve 2 is expressed as - |
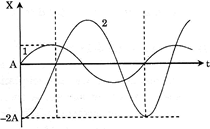 |
A) \[x=2A\,\sin \,\,(\omega t-\pi /2)\]
B) \[x=2A\,\sin \,\,(\omega t+\pi /2)\]
C) \[x=-\,2A\,\sin \,\,(\omega t-\pi /2)\]
D) \[x=A\sin \,\,(\omega t-\pi /2)\]
Correct Answer: A
Solution :
Oscillations represented by curve 2 lags in phase by \[\pi /2\] and the periods are same. Amplitude of curve 2 is double that of 1.You need to login to perform this action.
You will be redirected in
3 sec
