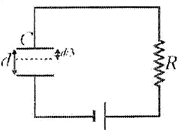
| A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant \[\kappa =2\]. The level of liquid is \[\frac{d}{3}\] initially. Suppose the liquid level decreases at a constant speed v, the time constant as a function of time \[t\] is |
 |
A) \[\frac{6{{\in }_{0}}R}{5d+3vt}\]
B) \[\frac{\left( 15d+9vt \right){{\in }_{0}}R}{2{{d}^{2}}-3dvt-9{{v}^{2}}{{t}^{2}}}\]
C) \[\frac{6{{\in }_{0}}R}{5d-3vt}\]
D) \[\frac{\left( 15d-9vt \right){{\in }_{0}}R}{2{{d}^{2}}-3dvt-9{{v}^{2}}{{t}^{2}}}\]
Correct Answer: A
Solution :
| at any time, the level of liquid \[{{x}_{1}}=\left( \frac{d}{3}-vt \right),\]and the thickness of the air \[{{x}_{2}}=d-\left( \frac{d}{3}-vt \right)=\left( \frac{2d}{3}+vt \right).\] |
| Now \[C=\frac{{{C}_{1}}{{C}_{2}}}{{{C}_{1}}+{{C}_{2}}};\]where \[{{C}_{1}}=\frac{{{\in }_{0}}kA}{{{x}_{1}}},\]and \[{{C}_{2}}=\frac{{{\in }_{0}}A}{{{x}_{2}}}.\] |
| Time constant \[\tau =CR=\left[ \frac{6{{\in }_{0}}R}{5d+3vt} \right]\] |
You need to login to perform this action.
You will be redirected in
3 sec
