A) \[{{\mu }_{1}}a={{\mu }_{2}}\,\alpha \]
B) \[{{\mu }_{1}}\,\alpha ={{\mu }_{2}}\,a\]
C) \[{{\mu }_{1}}\,b={{\mu }_{2}}\,\beta \]
D) \[{{\mu }_{1}}\,\beta ={{\mu }_{2}}\,b\]
Correct Answer: A
Solution :
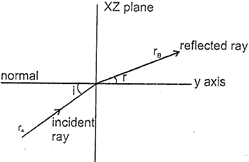 |
| We have \[\cos \theta =\frac{\vec{A}\cdot \vec{B}}{ab}\] Similarly here |
| \[\cos i=\frac{{{{\vec{r}}}_{A}}\cdot \hat{j}}{|{{r}_{A}}|\cdot |1|}=\frac{(a\hat{i}+b\hat{j})\cdot \hat{j}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}=\frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\] and \[\cos r=\frac{{{{\vec{r}}}_{B}}\cdot \hat{j}}{|{{r}_{B}}|\cdot |1|}\]\[=\frac{(\alpha \hat{i}+\beta \hat{j})\cdot \hat{j}}{\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}}=\frac{\beta }{\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}}\] |
| From shell's law\[{{\mu }_{1}}\sin i={{\mu }_{2}}\sin r\]\[\Rightarrow \]\[{{\mu }_{1}}\sqrt{1-{{\cos }^{2}}i}={{\mu }_{2}}\sqrt{1-{{\cos }^{2}}r}\]\[\Rightarrow \]\[{{\mu }_{1}}\sqrt{1-\frac{{{b}^{2}}}{{{b}^{2}}+{{a}^{2}}}}={{\mu }_{2}}\sqrt{1-\frac{{{\beta }^{2}}}{{{\alpha }^{2}}+{{\beta }^{2}}}}\] |
| \[\Rightarrow \]\[{{\mu }_{1}}\frac{a}{\sqrt{{{b}^{2}}+{{a}^{2}}}}={{\mu }_{2}}\frac{\alpha }{\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}}\] |
| both \[{{\vec{r}}_{A}}\] & \[{{\vec{r}}_{B}}\] are unit vectors so magnitudes of both vectors is 1 i.e. \[\sqrt{{{b}^{2}}+{{a}^{2}}}=\sqrt{{{\alpha }^{2}}+{{\beta }^{2}}}=I\] So \[{{\mu }_{1}}a={{\mu }_{2}}\alpha \] |
You need to login to perform this action.
You will be redirected in
3 sec
