question_answer

Let \[\left| \!{\overline {\,  {} \,}} \right. \]denotes a curve \[y=y(x)\] which is in the first quadrant and let the point (1, 0) lie on it. Let the tangent to \[\left| \!{\overline {\,  {} \,}} \right. \]at a point P intersect the v-axis at \[{{\text{Y}}_{{{\text{p}}^{\text{.}}}}}\]. If \[\text{P}{{\text{Y}}_{\text{p}}}\] has length 1 for each point P on \[\left| \!{\overline {\,  {} \,}} \right. \], then which of the following options is/are correct?

A) \[xy'-\,\sqrt{1-{{x}^{2}}}=\,0\]

B) \[y\,=\,-\,\text{lo}{{\text{g}}_{e}}\,\left( \frac{1+\sqrt{1-{{x}^{2}}}}{x} \right)+\,\sqrt{1-{{x}^{2}}}\]

C) \[xy'+\sqrt{1-{{x}^{2}}}=\,0\]

D) \[y\,=\,\text{lo}{{\text{g}}_{e}}\,\left( \frac{1+\sqrt{1\,\,-\,{{x}^{2}}}}{x} \right)-\,\sqrt{1-{{x}^{2}}}\]

Correct Answer: C , D

Solution :

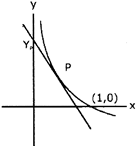Equation of Tangent at P

\[y-y=\frac{dy}{dx}\,(X-x)\]

For \[{{\text{Y}}_{p}}\]\[\Rightarrow \]\[(X=0)\]

\[{{Y}_{p}}=y-x\frac{dy}{dx}\]

Distance \[{{\text{Y}}_{\text{p}}}\text{P=1}\]

\[{{x}^{2}}+{{\left( y-y+x\frac{dy}{dx} \right)}^{2}}=1\]

\[{{x}^{2}}\left( 1+{{\left( \frac{dy}{dx} \right)}^{2}} \right)\,=\,1\]

\[{{\left( \frac{dy}{dx} \right)}^{2}}=\frac{1}{{{x}^{2}}}-1\]

\[\frac{dy}{dx}=\pm \frac{\sqrt{1-x}}{x}\to \]option A and C

\[\int{dy}=\pm \int{\frac{\sqrt{1-{{x}^{2}}}}{x}dx}\]

\[x=\text{sin}\theta \]

\[y=\pm \int{\frac{\cos \theta }{\sin \theta }}\cos \theta d\theta \]

\[y=\pm \int{\frac{1-{{\sin }^{2}}\theta }{\sin \theta }}d\theta \]

\[y=\pm \int{(cosec\theta -sin\theta )d\theta }\]

\[y=\pm (In\left| \cos ec\theta +\cot \theta \left| +\cos \theta  \right. \right.)+\text{C}\]

P as (1, 0) \[\Rightarrow \]\[C=0\]

\[y=\pm \left( \text{In}\left( \frac{1+\sqrt{1-{{x}^{2}}}}{x} \right) \right)+\sqrt{1-{{x}^{2}}}\]

\[\to \]option [b], [d],

Solution :

Same as Above