| Define the collections \[\{{{\text{E}}_{1}},{{\text{E}}_{2}},\,{{\text{E}}_{3}},\,....\}\]of ellipse and \[\{{{\text{R}}_{1}},\,{{\text{R}}_{2}},\,{{\text{R}}_{3}},\,.....\}\]of rectangles as follows: |
| \[{{\text{E}}_{1}}\,:\,\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{4}\,=\,1\] |
| \[{{\text{R}}_{1}}\,:\] rectangle of largest area, with sides parallel to the axes, inscribed in \[{{\text{E}}_{1}};\] |
| \[{{E}_{n}}\ :\]ellipse \[\frac{{{x}^{2}}}{a_{n}^{2}}+\frac{{{y}^{2}}}{b_{n}^{2}}=\,1\]of largest area inscribed in |
| \[{{\text{R}}_{n-1}},\,n\,>\,1\,;\] |
| \[{{\text{R}}_{n}}\,:\] rectangle of largest area, with sides parallel to the axes inscribed in \[{{\text{E}}_{n}},\,n\,>\,1\] |
| Then which of the following options is/are correct? |
A) The eccentricities of \[{{\text{E}}_{18}}\] and \[{{\text{E}}_{19}}\] are not equal
B) The distance of a focus from the centre in \[{{\text{E}}_{9}}\] is \[\frac{\sqrt{5}}{32}\]
C) \[\sum\limits_{n\,=\,1}^{\text{N}}{{}}\]\[(area\,of\,{{\text{R}}_{n}})\,<24,\] for each positive integer N
D) The length of latus rectum of \[{{\text{E}}_{9}}\] is \[\frac{1}{6}\]
Correct Answer: C , D
Solution :
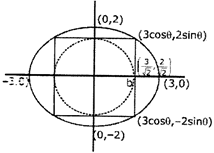 |
| \[{{\text{E}}_{1}}\,\Rightarrow \frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{4}=1\] |
| \[l=6\,\text{cos}\theta \] |
| \[\text{b}=4\,\text{sin}\theta \] |
| Area \[=12\times \text{sin}2\theta \] |
| \[{{\text{A}}_{\text{max}}}=12\] |
| \[\text{sin}\,2\theta \,=1\] |
| \[2\theta =\frac{\pi }{2}\] |
| \[\theta =\frac{\pi }{4}\] |
| \[{{\text{E}}_{2}}:a\,=\frac{3}{\sqrt{2}};b=\frac{2}{\sqrt{2}}:\]\[a=3;r=\frac{1}{\sqrt{2}};\text{b}=2;r=\frac{1}{\sqrt{2}}\] |
| (i) \[{{e}^{2}}=1-\frac{{{b}^{2}}}{{{a}^{2}}}\]eccentricities of all ellipse will be equal |
| (ii) For \[{{\text{E}}_{9}};\]\[e=\frac{\sqrt{5}}{3}\]and \[a=3\times {{\left( \frac{1}{\sqrt{2}} \right)}^{8}}\] |
| \[\therefore \] distance of focus from centre \[=ae=\frac{3}{16}\times \frac{\sqrt{5}}{3}=\frac{\sqrt{5}}{16}\] |
| (iii) sum of area of rectangles \[=12+6+3+...\] |
| \[\text{A}=\frac{12}{1-\frac{1}{2}}=24\] |
| (iv) \[\text{L}\text{.R}.=\frac{2{{b}^{2}}}{a}=\frac{2\times {{\left( 2\times \frac{1}{16} \right)}^{2}}}{2.\frac{1}{16}}=\frac{2\times \frac{1}{64}}{3\times \frac{1}{16}}=\frac{1}{6}.\] |
Solution :
Same as aboveYou need to login to perform this action.
You will be redirected in
3 sec
