question_answer

The tangent at a point whose eccentric angle \[60{}^\circ \] on the ellipse \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\,\,(a>b)\] meet the auxiliary circle at L and M. If LM subtends a right angle at the centre, then eccentricity of the ellipse is-

A) \[\frac{1}{\sqrt{7}}\]                             

B) \[\frac{2}{\sqrt{7}}\]

C) \[\frac{3}{\sqrt{7}}\]                             

D) \[\frac{1}{2}\]

Correct Answer: B

Solution :

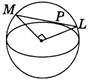
[B]

Point P will be \[(a\cos 60{}^\circ ,b\sin 60{}^\circ )\]
Tangent will be \[\frac{x\cos 60{}^\circ }{a}+\frac{y\sin 60{}^\circ }{b}=1\]
\[\frac{x}{2a}+\frac{y\sqrt{3}}{2b}=1\]	?(1)
Homogenise \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] with the help of eqn. (1) We get \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}{{\left[ \frac{x}{2a}+\frac{y\sqrt{3}}{2b} \right]}^{2}}\]
\[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\left[ \frac{{{x}^{2}}}{4{{a}^{2}}}+\frac{3{{y}^{2}}}{4{{b}^{2}}}+\frac{xy\sqrt{3}}{2ab} \right]\]
\[\frac{3{{x}^{2}}}{4}+{{y}^{2}}\left( 1-\frac{3{{a}^{2}}}{4{{b}^{2}}} \right)-\frac{a\sqrt{3}xy}{2b}=0\]
For \[90{}^\circ \] at center \[\frac{3}{4}+1-\frac{3{{a}^{2}}}{4{{b}^{2}}}=0\]
\[\frac{3}{4}\,\,\,\frac{{{a}^{2}}}{{{a}^{2}}(1-{{e}^{2}})}=\frac{7}{4}\]
\[1-{{e}^{2}}=\frac{3}{7}\Rightarrow {{e}^{2}}=\frac{4}{7}\Rightarrow e=\frac{2}{\sqrt{7}}\]