A) \[\frac{\pi }{2}<I<\frac{{{\pi }^{2}}}{4}\]
B) \[\frac{\pi }{4}<I<\frac{{{\pi }^{2}}}{2}\]
C) \[1<I<\frac{\pi }{2}\]
D) \[0<I<1\]
Correct Answer: A
Solution :
[A] 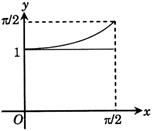 |
| Since, \[\sin x\frac{dy}{dx}+y\cos x=1\] |
| \[\frac{dy}{dx}+y\cot x=\text{cosec}\,x\] |
| IF \[(e=Ns\,\,B\,\,\omega \,\,\sin \,\,\omega t),\] \[y\sin x=\int{\text{cosec}\,x.\,\sin x\,\,dx}\] |
| \[y\sin x=x+C\] |
| If \[x\to 0,\] y is finite \[\therefore C=O\] |
| \[\therefore y=\frac{x}{\sin x}\] |
| Now, \[I<\frac{{{\pi }^{2}}}{4}\] and \[I>\frac{\pi }{2}\] |
| Hence, \[\frac{\pi }{2}<I<\frac{{{\pi }^{2}}}{4}\] |
You need to login to perform this action.
You will be redirected in
3 sec
