A) \[\frac{L{{E}^{2}}}{2R_{2}^{2}}\]
B) \[\frac{L{{E}^{2}}}{2R_{1}^{2}}\]
C) \[\frac{L{{E}^{2}}}{2{{R}_{1}}{{R}_{2}}}\]
D) \[\frac{L{{E}^{2}}{{({{R}_{1}}+{{R}_{2}})}^{2}}}{2R_{1}^{2}R_{2}^{2}}\]
Correct Answer: B
Solution :
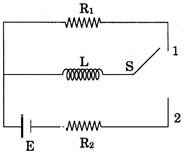
[A] When the key is at position (2) for a long time; the energy stored in the inductor is: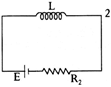 \[{{U}_{B}}=\frac{1}{2}L{{i}_{{{O}^{2}}}}=\frac{1}{2}.L.{{\left( \frac{E}{{{R}_{2}}} \right)}^{2}}=\frac{L.E{{.}^{2}}}{2{{R}_{2}}^{2}}\] This whole energy will be dissipated in the form of heat when the inductor is connected to \[{{R}_{1}}\] and no source is connected.
\[{{U}_{B}}=\frac{1}{2}L{{i}_{{{O}^{2}}}}=\frac{1}{2}.L.{{\left( \frac{E}{{{R}_{2}}} \right)}^{2}}=\frac{L.E{{.}^{2}}}{2{{R}_{2}}^{2}}\] This whole energy will be dissipated in the form of heat when the inductor is connected to \[{{R}_{1}}\] and no source is connected.
You need to login to perform this action.
You will be redirected in
3 sec
