| Solve the following system of equations by matrix method when \[x\ne 0,\,\]\[y\ne 0\] and \[z\ne 0.\] |
| \[\frac{2}{x}-\frac{3}{y}+\frac{3}{z}=10,\] \[\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=10\] |
| and \[\frac{3}{x}-\frac{1}{y}+\frac{2}{z}=13\] |
| OR |
| The sum of three numbers is 6. Twice the third number when added to the first number gives 7. On adding the sum of the second and third numbers to thrice the first number, we get 12. Find the numbers, using matrix method. |
Answer:
Given system of equations is
\[\frac{2}{x}-\frac{3}{y}+\frac{3}{z}=10\] ? (i)
\[\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=10\] ? (ii)
and \[\frac{3}{x}-\frac{1}{y}+\frac{2}{z}=13\] ? (iii)
Given equations can be written in matrix form as
\[AX=B\]
Where, \[A=\left[ \begin{matrix} 2 & -\,3 & 3 \\ 1 & 1 & 1 \\ 3 & -\,1 & 2 \\ \end{matrix} \right],\] \[X=\left[ \begin{matrix} 1/x \\ 1/y \\ 1/z \\ \end{matrix} \right]\] and
\[B=\left[ \begin{matrix} 10 \\ 10 \\ 13 \\ \end{matrix} \right]\]
Now, \[|A|\,\,=\left| \begin{matrix} 2 & -\,3 & 3 \\ 1 & 1 & 1 \\ 3 & -1 & 2 \\ \end{matrix} \right|=2\,(2+1)+3(2-3)+3(-1-3)\]
\[=6-3-12=-\,9\ne 0\]
\[\therefore \] \[{{A}^{-\,1}}\]exists.
Now, cofactors of elements of \[|A|\] are
\[{{C}_{11}}={{(-\,1)}^{2}}\left| \begin{matrix} 1 & 1 \\ -\,1 & 2 \\ \end{matrix} \right|=2+1=3\]
\[{{C}_{12}}={{(-\,1)}^{3}}\left| \begin{matrix} 1 & 1 \\ 3 & 2 \\ \end{matrix} \right|=-(2-3)=1\]
\[{{C}_{13}}={{(-\,1)}^{4}}\left| \begin{matrix} 1 & 1 \\ 3 & -\,1 \\ \end{matrix} \right|=-\,1-3=-\,4\]
\[{{C}_{21}}={{(-\,1)}^{3}}\left| \begin{matrix} -\,3 & 3 \\ -\,1 & 2 \\ \end{matrix} \right|=-\,(-\,6+3)=3\]
\[{{C}_{22}}={{(-\,1)}^{4}}\left| \begin{matrix} 2 & 3 \\ 3 & 2 \\ \end{matrix} \right|=4-9=-\,5\]
\[{{C}_{23}}={{(-1)}^{5}}\left| \begin{matrix} 2 & -\,3 \\ 3 & -1 \\ \end{matrix} \right|=-(-\,2+9)=-7\]
\[{{C}_{31}}={{(-\,1)}^{4}}\left| \begin{matrix} -\,3 & 3 \\ 1 & 1 \\ \end{matrix} \right|=-3-3=-\,6\]
\[{{C}_{32}}={{(-\,1)}^{5}}\left| \begin{matrix} 2 & 3 \\ 1 & 1 \\ \end{matrix} \right|=-(2-3)=1\]
\[{{C}_{33}}={{(-\,1)}^{6}}\left| \begin{matrix} 2 & -3 \\ 1 & 1 \\ \end{matrix} \right|=2+3=5\]
\[\therefore \] \[{{A}^{-1}}=\frac{1}{|A|}\text{adj}\,(A)\].
\[=\frac{1}{|A|}\left[ \begin{matrix} {{C}_{11}} & {{C}_{21}} & {{C}_{31}} \\ {{C}_{12}} & {{C}_{22}} & {{C}_{32}} \\ {{C}_{13}} & {{C}_{23}} & {{C}_{33}} \\ \end{matrix} \right]=\frac{1}{-\,9}\left[ \begin{matrix} 3 & 3 & -\,6 \\ 1 & -\,5 & 1 \\ -\,4 & -\,7 & 5 \\ \end{matrix} \right]\]
\[\because \] \[X={{A}^{-1}}B\]
\[\therefore \] \[\left[ \begin{matrix} 1/x \\ 1/y \\ 1/z \\ \end{matrix} \right]=-\frac{1}{9}\left[ \begin{matrix} 3 & 3 & -\,6 \\ 1 & -\,5 & 1 \\ -\,4 & -\,7 & 5 \\ \end{matrix} \right]\,\,\left[ \begin{matrix} 10 \\ 10 \\ 13 \\ \end{matrix} \right]\]
\[\Rightarrow \]\[\left[ \begin{matrix} 1/x \\ 1/y \\ 1/z \\ \end{matrix} \right]=-\frac{1}{9}\left[ \begin{matrix} 30+30-78 \\ 10-50+13 \\ -\,40-70+65 \\ \end{matrix} \right]=-\frac{1}{9}\left[ \begin{matrix} -\,18 \\ -\,27 \\ -\,45 \\ \end{matrix} \right]=\left[ \begin{matrix} 2 \\ 3 \\ 5 \\ \end{matrix} \right]\]
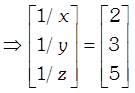
On comparing the corresponding elements, we get
\[\frac{1}{x}=2\] \[\Rightarrow \] \[x=\frac{1}{2}\]
\[\frac{1}{y}=3\] \[\Rightarrow \] \[y=\frac{1}{3}\]
and \[\frac{1}{z}=5\] \[\Rightarrow \] \[z=\frac{1}{5}\]
OR
Let the first, second and third numbers be x, y, z respectively. Then,
\[x+y+z=6\] ? (i)
\[x+2z=7\] ? (ii)
\[3x+y+z=12\] ? (iii)
Let \[A=\left[ \begin{matrix} 1 & 1 & 1 \\ 1 & 0 & 2 \\ 3 & 1 & 1 \\ \end{matrix} \right],\] \[x=\left[ \begin{align} & x \\ & y \\ & z \\ \end{align} \right]\] and \[B=\left[ \begin{align} & 6 \\ & 7 \\ & 12 \\ \end{align} \right]\]
Then, the given system in matrix form is AX = B.
Now, \[|A|=\left[ \begin{matrix} 1 & 1 & 1 \\ 1 & 0 & 2 \\ 3 & 1 & 1 \\ \end{matrix} \right]=\left[ \begin{matrix} 1 & 1 & 1 \\ 0 & -\,1 & 1 \\ 0 & -\,2 & -\,2 \\ \end{matrix} \right]\]
\[\left[ \begin{matrix} {{R}_{2}}\to {{R}_{2}}-{{R}_{1}}; \\ {{R}_{3}}\to {{R}_{3}}-3{{R}_{1}} \\ \end{matrix} \right]\]
\[=1.(2+2)=4\ne 0\]
\[\therefore \] A is invertible.
So, the given system has a unique solution, \[X={{A}^{-1}}B.\]
The minors of the elements of |A| are
\[{{M}_{11}}=-\,2,\] \[{{M}_{12}}=-\,5,\] \[{{M}_{13}}=1;\]
\[{{M}_{21}}=0,\] \[{{M}_{22}}=-\,2,\] \[{{M}_{23}}=-\,2;\]
\[{{M}_{31}}=2,\] \[{{M}_{32}}=1,\] \[{{M}_{33}}=-\,1.\]
The cofactors of the elements of |A| are
\[{{A}_{11}}=-\,2,\] \[{{A}_{12}}=5,\] \[{{A}_{12}}=1;\]
\[{{A}_{21}}=0,\] \[{{A}_{22}}=-\,2,\] \[{{A}_{23}}=2;\]
\[{{A}_{31}}=2,\] \[{{A}_{32}}=-\,1,\] \[{{A}_{33}}=-\,1\]
\[\therefore \] \[(adj\,A)=\left[ \begin{matrix} -\,2 & 5 & 1 \\ 0 & -\,2 & 2 \\ 2 & -\,1 & -\,1 \\ \end{matrix} \right]=\left[ \begin{matrix} -\,2 & 0 & 2 \\ 5 & -\,2 & -\,1 \\ 1 & 2 & -\,1 \\ \end{matrix} \right]\]
\[\Rightarrow \] \[{{A}^{-1}}=\frac{1}{|A|}\cdot (adj\,A)=\frac{1}{4}\left[ \begin{matrix} -\,2 & 0 & 2 \\ 5 & -\,2 & -\,1 \\ 1 & 2 & -\,1 \\ \end{matrix} \right]\]
\[\Rightarrow \] \[X={{A}^{-1}}B\]
\[\Rightarrow \] \[\left[ \begin{align} & x \\ & y \\ & z \\ \end{align} \right]=\frac{1}{4}\cdot \left[ \begin{matrix} -\,2 & 0 & 2 \\ 5 & -\,2 & -\,1 \\ 1 & 2 & -\,1 \\ \end{matrix} \right]\left[ \begin{matrix} 6 \\ 7 \\ 12 \\ \end{matrix} \right]\]
\[=\frac{1}{4}\cdot \left[ \begin{matrix} -\,12+0+24 \\ 30-14-12 \\ 6+14-12 \\ \end{matrix} \right]\] \[=\frac{1}{4}\cdot \left[ \begin{matrix} 12 \\ 4 \\ 8 \\ \end{matrix} \right]=\left[ \begin{matrix} 3 \\ 1 \\ 2 \\ \end{matrix} \right]\]
\[\Rightarrow \] x = 3, y = 1, z = 2
Hence, the required numbers are 3, 1, 2.
You need to login to perform this action.
You will be redirected in
3 sec
