question_answer

Find the area of the region bounded by the curves

\[{{y}^{2}}=4ax\] and \[{{x}^{2}}=4ay.\]

OR

Using integration, find the area of the triangular region whose sides have the equation \[y=2x+1,\]\[y=3x+1\] and x = 4.

Answer:

The given curves are

\[{{y}^{2}}=4ax\]  [right parabola]         ?(i)

and       \[{{x}^{2}}=4ay\]  [upward parabola]   ...(ii)

On squaring both sides of Eq. (i), we get

\[{{({{y}^{2}})}^{2}}={{(4ax)}^{2}}\]

\[\Rightarrow \]   \[{{y}^{4}}=16{{a}^{2}}{{x}^{2}}\]

\[\Rightarrow \]   \[{{y}^{4}}=16{{a}^{2}}(4ay)\]                    [from Eq. (ii)]

\[\Rightarrow \]   \[y({{y}^{3}}-64{{a}^{3}})=0\]

\[\Rightarrow \]   y = 0, \[{{y}^{3}}={{(4a)}^{3}}\] \[\Rightarrow \] y = 0, y = 4a

When    \[y=0,\] then x = 0

When    y = 4a, then x = 4a

Thus, the given parabolas intersect each other at

0(0, 0) and A(4a, 4a). Then, the shaded part in the figure is the required area.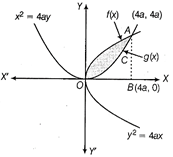

For the curve \[{{y}^{2}}=4ax,\]

\[y=2\sqrt{a}\sqrt{x}=f(x)\,\,(\text{say)}\]

and for the curve \[{{x}^{2}}=4ay,\]

\[y=\frac{{{x}^{2}}}{4a}=g(x)(\text{say})\]

\[\therefore \]  Required area = Area of shaded region OACO

\[=\int_{0}^{4a}{[f(x)-g(x)]}\,dx\]

\[=\int_{0}^{4a}{2\sqrt{a}\sqrt{x}dx-\int_{0}^{4a}{\frac{{{x}^{2}}}{4a}dx}}\]

\[=2\sqrt{a}\left[ \frac{{{x}^{3/2}}}{3/2} \right]_{0}^{4a}-\frac{1}{4a}\left[ \frac{{{x}^{3}}}{3} \right]_{0}^{4a}\]

\[=\frac{4}{3}\sqrt{a}{{(4a)}^{3/2}}-\frac{1}{12}{{(4a)}^{3}}\]

\[=\frac{32{{a}^{2}}}{3}-\frac{16{{a}^{2}}}{3}=\frac{16{{a}^{2}}}{3}\] sq units

OR

We have to find the triangular region area whose equations of sides of triangle are given as

\[Y=2x+1\]                               ?(i)

\[Y=3x+1\]                               ?(ii)

and       x = 4                                        ?(iii)

The line \[y=2x+1\]passes through the points (0, 1) and (1, 3) and the line \[y=3x+1\] passes through the points (0, 1) and (1, 4).

Now, subtracting Eq. (i) from Eq. (ii), we get

x = 0 \[\Rightarrow \] \[y=2(0)+1=1\]

So, lines \[y=2x+1\] and \[y=3x+1\] meet at the point A (0, 1).

Again, solving Eqs. (ii) and (iii), we get

\[y=3x+1\] \[\Rightarrow \]\[y=3(4)+1\]     \[[\because \,\,\,x=4]\]

\[\Rightarrow \]   \[y=12+1=13\]

So, lines \[y=3x+1\] and x = 4 meet at the point C (4, 13).

On solving Eqs. (i) and (iii), we get

\[y=2x+1\] \[\Rightarrow \]\[y=2(4)+1\]  \[[\because \,\,\,x=4]\]

\[y=8+1=9\]

So, lines \[y=2x+1\] and x = 4 meet at the point B (4, 9).

Graph of the required region is given below:

We have to find the area of \[\Delta \,ABC\] shaded above.

Hence, required area of \[\Delta \,ABC\]

\[=\text{Area}\,\,\text{of}\,\,AOHC-\text{Area}\,\,\text{of}\,\,AOHB\]

\[=\int_{0}^{4}{(3x+1)\,dx-\int_{0}^{4}{(2x+1)\,dx}}\]

\[=\left[ \frac{3{{x}^{2}}}{2}+x \right]_{0}^{4}-\left[ \frac{2{{x}^{2}}}{2}+x \right]_{0}^{4}\]

\[=\left[ \frac{3(16)}{2}+4 \right]-[16+4]\]

\[=24+4-16-4=8\,\text{sq}\,\,\text{units}\]