question_answer

In a quadrilateral ABCD, DO and CO are the bisectors of \[\angle D\] and  \[\angle C\] respectively.

Prove that \[\angle COD=\frac{1}{2}[\angle A+\angle B].\]

Answer:

In\[\Delta COD\], we have

\[\angle COD+\angle \text{1}+\angle 2=180{}^\circ \]

\[\Rightarrow \]   \[\angle COD\,=180{}^\circ -[\angle 1+\angle 2]\]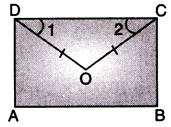

\[\Rightarrow \]\[\angle COD\,=180{}^\circ -\left[ \frac{1}{2}\angle D+\frac{1}{2}\angle C \right]\]

\[\Rightarrow \]\[\angle COD\,=180{}^\circ -\frac{1}{2}[\angle D+\angle C]\]

But                  \[\angle A+\angle B+\angle C+\angle D=360{}^\circ \]

\[\Rightarrow \]   \[\angle C+\angle D=360{}^\circ -(\angle A+\angle B)\]

\[\Rightarrow \]   \[\angle COD=180{}^\circ -\frac{1}{2}[360{}^\circ -(\angle A+\angle B)]\]

\[=\text{ }180{}^\circ -\frac{1}{2}\text{  }\left[ 360{}^\circ  \right]\text{ }+\text{ }\frac{1}{2}\text{ }\left[ \angle A\text{ }+\text{ }\angle B \right]\]

\[=\text{ }180{}^\circ -180{}^\circ \text{ }+\text{ }\frac{1}{2}\text{ }\left[ \angle A\text{ }+\text{ }\angle B \right]\]

\[=\frac{1}{2}(\angle A+\angle B)\]

Thus,           \[\angle COD=\frac{1}{2}[\angle A+\angle B]\]