question_answer

A variable plane which remains at a constant distance 3p from the origin cut the coordinate axes at A, B and C. Show that the locus of the centroid of \[\Delta ABC\] is \[{{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}={{p}^{-2}}.\]

OR

If the lines \[\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\] and \[\frac{x-3}{2}=\frac{y-k}{2}=\frac{z}{1}\]  intersect, find the value of k and hence, find the equation of the plane containing these lines.

Answer:

Let the equation of plane in intercept form be

\[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\] \[\Rightarrow \] \[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}-1=0\]      ...(i)

It cut the axes on the point A(a, 0, 0), B(0, b, 0)and (0, 0, c).

Let \[(\alpha ,\,\,\beta ,\,\,\gamma )\] be the centroid of \[\Delta ABC.\] Then,

\[\alpha =\frac{a+0+0}{3},\] \[\beta =\frac{0+b+0}{3}\] and \[\gamma =\frac{0+0+c}{3}\]

\[\Rightarrow \] \[a=3\alpha ,\] \[b=3\beta \] and \[c=3\gamma \]

Now, the perpendicular distance from origin (0, 0, 0) to the plane (i) is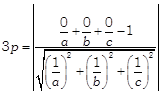

\[\Rightarrow \]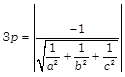

\[\Rightarrow \]   \[\frac{1}{3p}=\sqrt{\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}}\]

On squaring both sides, we get

\[\frac{1}{9{{p}^{2}}}=\frac{1}{{{a}^{2}}}+\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}\]

On putting the values of a, b and c, we get

\[\frac{1}{9{{p}^{2}}}=\frac{1}{{{(3\alpha )}^{2}}}+\frac{1}{{{(3\beta )}^{2}}}+\frac{1}{{{(3\gamma )}^{2}}}\]

\[\Rightarrow \]   \[\frac{1}{9{{p}^{2}}}=\frac{1}{9{{\alpha }^{2}}}+\frac{1}{9{{\beta }^{2}}}+\frac{1}{9{{\gamma }^{2}}}\]

\[\Rightarrow \]   \[\frac{1}{9{{p}^{2}}}=\frac{1}{9}\left( \frac{1}{{{\alpha }^{2}}}+\frac{1}{{{\beta }^{2}}}+\frac{1}{{{\gamma }^{2}}} \right)\]

\[\Rightarrow \]   \[\frac{1}{{{p}^{2}}}=\frac{1}{{{\alpha }^{2}}}+\frac{1}{{{\beta }^{2}}}+\frac{1}{{{\gamma }^{2}}}\]

Hence, the locus of the centroid \[(\alpha ,\,\,\beta ,\,\,\gamma )\] is

\[\frac{1}{{{p}^{2}}}=\frac{1}{{{x}^{2}}}+\frac{1}{{{y}^{2}}}+\frac{1}{{{z}^{2}}}\]                \[[\text{replace}\,\,\alpha ,\,\,\beta ,\,\,\gamma \,\,by\,\,x,\,\,y,\,\,z]\]

\[\therefore \] \[{{p}^{-2}}={{x}^{-2}}+{{y}^{-2}}+{{z}^{-2}}\]             Hence proved.

OR

Given equation of lines are

\[\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\]               ?(i)

and       \[\frac{x-3}{1}=\frac{y-k}{2}=\frac{z}{1}\]                                ?(ii)

Since, these lines intersect therefore the shortest distance between them will be zero.

Now, comparing these lines with

\[\frac{x-{{x}_{1}}}{{{a}_{1}}}=\frac{y-{{y}_{1}}}{{{b}_{1}}}=\frac{z-{{z}_{1}}}{{{c}_{1}}}\]

and \[\frac{x-{{x}_{2}}}{{{a}_{2}}}=\frac{y-{{y}_{2}}}{{{b}_{2}}}=\frac{z-{{z}_{2}}}{{{c}_{2}}},\] we get

\[{{x}_{1}}=1,\] \[{{y}_{1}}=-\,1,\] \[{{z}_{1}}=1\]

\[{{x}_{2}}=3,\] \[{{y}_{2}}=k,\] \[{{z}_{2}}=0\]

\[{{a}_{1}}=2,\] \[{{b}_{1}}=3,\] \[{{c}_{1}}=4\]

\[{{a}_{2}}=1,\] \[{{b}_{2}}=2,\] \[{{c}_{2}}=1\]

We know that if two lines intersect, then shortest distance between them = 0

\[\therefore \]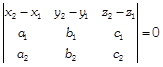

\[\therefore \] 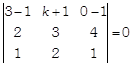 \[\Rightarrow \]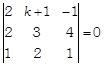

\[\Rightarrow \]   \[2(3-8)-(k\,+1)(2-4)-1(4-3)=0\]

\[\Rightarrow \]   \[2(-\,5)-(k+1)(-\,2)-1(1)=0\]

\[\Rightarrow \]   \[-\,10+2(k+1)-1=0\]

\[\Rightarrow \]   \[2(k+1)=11\]

\[\Rightarrow \]   \[k=\frac{11}{2}-1=\frac{9}{2}\]

Now, let the required equation of plane be

\[A(x-1)+B(y+1)+C(z-1)=0\]

where, A, B and C are DR's ratios of normal and \[(1,\,\,-\,1,\,\,1)\] is the point on the line (i)

[\[\therefore \] equation of plane is \[A(x-{{x}_{1}})+B(y-{{y}_{1}})+C(z-{{z}_{1}})=0\]]

As we know that, the normal to the plane is also a normal to the lines lying in that plane, therefore

\[2A+3B+4C=0\]

and       \[A+2B+C=0\]

\[[\because \,\,{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}=0]\]

On solving above equations, we get

\[\frac{A}{3-8}=\frac{-\,B}{2-4}=\frac{C}{4-3}\]

\[\Rightarrow \]   \[\frac{A}{-\,5}=\frac{-\,B}{-\,2}=\frac{C}{1}\] \[\Rightarrow \] \[\frac{A}{-\,5}=\frac{B}{2}=\frac{C}{1}\]

Thus, the required equation of the plane is

\[-\,5(x\,-1)+2(y\,+1)+1(z\,-1)=0\]

\[\Rightarrow \]   \[-\,5x+5+2y+2+z-1=0\]

\[\Rightarrow \]   \[5x-5-2y-2-z+1=0\]

\[\Rightarrow \]   \[5x-2y-z=6\]