question_answer

A string is wrapped several times round a solid cylinder and then the end of the string is held stationary while the cylinder is released from rest. The acceleration of the cylinder and tension in the string will be

A)  \[\frac{2g}{3}\]and\[\frac{mg}{3}\]             

B) \[g\]and \[\frac{mg}{2}\]

C) \[\frac{g}{3}\]and \[\frac{mg}{2}\]               

D)  \[\frac{g}{2}\]and\[\frac{mg}{3}\]  

Correct Answer: A

Solution :

Let a be the acceleration of the cylinder and \[\alpha \]be its angular acceleration. Invoking \[\tau =I\alpha \]about the center of the cylinder, we get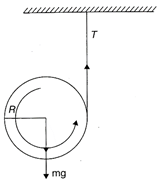 \[TR=Ia=\left( \frac{m{{R}^{2}}}{2} \right)\alpha \] As the string unwinds without slipping, so \[a=R\alpha \] Also, \[{{F}_{ext}}=m{{a}_{cm}}\] \[\therefore \]\[mg-T=ma\] Solving these equations, we have \[a=\frac{2}{3}g\]and \[T=\frac{mg}{3}\] Hence, the correction option is [a].