question_answer

A small bulb is placed at the bottom of a tank, containing water at a depth of 80 cm. What is the area of the surface of water, through which light from the bulb can emerge out? Refractive index of water is 4/3.

Answer:

The light rays coming from bulb can pass through the surface, if angle of incidence at surface is less than or equal to critical angle (c) for water-air interface. If h is depth of bulb from the surface, then light will emerge only through a circle of radius r given by 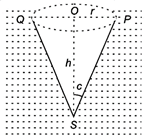Critical angle for water-air interface From the diagram,          \[r=h\,\,tan\,c\]   ...(i) where depth,                  h = 80 cm = 0.80 m but        \[\sin c=\frac{1}{{}_{a}{{n}_{w}}}=\frac{3}{4}\] 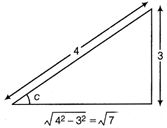Right angle triangle \[\therefore \]      \[\tan \,c=\frac{3}{\sqrt{7}}\] \[\therefore \] Radius,    \[t=h\tan c\]       [from Eq.(i)]                         \[=0.80\times 3/\sqrt{7}\] \[\therefore \] Area of circular surface of water, \[A=\pi {{r}^{2}}\] \[=3.14\times {{\left( 0.8\times \frac{3}{\sqrt{7}} \right)}^{2}}=3.14\times 0.64\times \frac{9}{7}\] \[=2.6\,{{m}^{2}}\]