question_answer

There identical capacities \[{{C}_{1}},{{C}_{2}}\] and \[{{C}_{3}}\] of capacitance \[6\mu F,\] each one is connected to a 12 V battery as shown in figure.

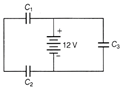
(i) Charge on each capacitor

(ii) Equivalent capacitance of the network

(iii) Energy stored in the network of capacitor

Answer:

(i) Capacitors \[{{C}_{1}}\] and \[{{C}_{2}}\] are in series across the 12 V supply. Equivalent capacitance of \[{{C}_{1}}\] and \[{{C}_{2}},\] \[{{C}_{eq}}=\frac{{{C}_{1}}\,{{C}_{2}}}{{{C}_{2}}+{{C}_{2}}}\] \[{{C}_{eq}}=\frac{6\times 6}{6+6}=3\mu F\] Charges of \[{{C}_{1}}\] and \[{{C}_{2}}\] are equal as they are in series, \[{{q}_{1}}={{q}_{2}}={{C}_{eq}}V=3\mu F\times 12=36\times {{10}^{-6}}C=36\mu C\] Charge on capacitor \[{{C}_{3}},{{q}_{3}}={{C}_{3}}V\]             \[=6\mu F\times 12=72\mu F\] (ii) Equivalent capacitance of the network, 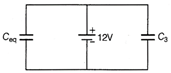\[{{C}_{eff}}={{C}_{eq}}+C=3+6=9\mu F\] (iii) Energy stored in the network \[=\frac{1}{2}{{C}_{eff}}{{V}^{2}}=\frac{1}{2}\times 9\times {{10}^{-6}}\times {{12}^{2}}\]             \[=6.48\times {{10}^{-4}}\,J\]