question_answer

Using Bohr's postulates for hydrogen atom, show that the total energy (E) of the electron in the stationary states can

be expressed as the sum of kinetic energy (K) and potential energy (U). Show that, \[K=-U/2.\]

Answer:

The energy E of an electron in an orbit is the sum of kinetic and potential energies. Let us consider a nucleus has charge Ze and an electron e is moving it in a circular path of radius \[r.\]The electrostatic force on the electron, 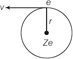\[F=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{Ze.e}{{{r}^{2}}}\] [According to Coulomb?s law] Since, electron is moving in a circular orbit. Centripetal force on the electron, \[F=m{{v}^{2}}\,/\,r.\] Where, \[m\]= mass of electron And \[v\]= speed of the electron. Hence, \[\frac{Z{{e}^{2}}}{4\pi {{\varepsilon }_{0}}{{r}^{2}}}=\frac{m{{v}^{2}}}{r}\] \[\therefore \]      \[r=\frac{Z{{e}^{2}}}{4\pi {{\varepsilon }_{0}}m{{v}^{2}}}\]                        ??? (i) According to Bohr?s quantisation postulates, the angular momentum of the electron, in nth orbit, \[mvr=n.\frac{h}{2\pi }\]                        ???.. (ii) From Eqs. (i) and (ii), we get \[v=\frac{Z{{e}^{2}}}{2{{\varepsilon }_{0}}hn}\]                    ???. (iii) \[\therefore \] Kinetic energy \[=\frac{1}{2}\,m{{v}^{2}}=\frac{m{{Z}^{2}}{{e}^{4}}}{8\varepsilon _{0}^{2}{{h}^{2}}}\,\left( \frac{1}{{{n}^{2}}} \right)\] In terms of Rydberg constant R, its simplified form is \[KE=\frac{Rhc}{{{n}^{2}}}\]  ?? (iv) \[\left[ \therefore \,\,R=\frac{m{{e}^{4}}}{8\varepsilon _{0}^{2}c{{h}^{3}}} \right]\] The potential energy of the electron in an orbit of radius \[r\] due to the electrostatic attraction by the nucleus is given by \[U=\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{(Ze)\,(-\,e)}{r}=-\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{Z{{e}^{2}}}{r}\] Putting the value of r from Eq. (i) and in terms of Rydberg constant R, its simplified form is \[U=-\frac{2Rhc}{{{n}^{2}}}\] ???.. (v) The total energy of the electron is therefore, \[E=KE+U\] \[=\frac{Z{{e}^{2}}}{8\pi {{\varepsilon }_{0}}r}-\frac{Z{{e}^{2}}}{4\pi {{\varepsilon }_{0}}r}=\frac{Z{{e}^{2}}}{8\pi {{\varepsilon }_{0}}r}\] Substituting for r from Eq. (i), we get \[E=-\frac{m{{Z}^{2}}{{e}^{4}}}{8{{\varepsilon }_{0}}^{2}{{h}^{2}}}\,\left( \frac{1}{{{n}^{2}}} \right)=\frac{-Rhc}{{{n}^{2}}}\] Where, n = 1, 2, 3,.... This is the expression for the energy of the electron in the nth orbit. For hydrogen atom \[Z=1,\] substituting the standard values, we get \[{{E}_{n}}=\frac{-13.6}{{{n}^{2}}}eV.\]Negative energy of the electron shows that the electron is bound to the nucleus and is not free to leave it. From Eqs. (iv) and (v), we get \[K=\frac{-\,U}{2}\]