| What do you understand by "sharpness of resonance" in a series L-C-R circuit? Write expression for Q-factor of the circuit. |
| Or |
| The magnetic flux passing perpendicular to the plane of a coil and directed into the paper is given by \[\phi =5{{t}^{2}}+6t+2,\] where \[\phi \] is in milliwebers and t in seconds. |
| (i) What is the magnitude of the induced emf set up in the loop, t = 1 s? |
| (ii) What is the direction of current through the resistor R? |
Answer:
Or (i) E = 16 m V The sharpness of resonance is given by \[={{\omega }_{0}}/2\Delta \omega \] where, \[{{\omega }_{0}}=\] resonance frequency \[\Delta \omega =\] bandwidth of the circuit The smaller the \[\Delta \omega ,\] sharper or narrower is the resonance. The quality factor Q is defined by \[Q=\frac{{{\omega }_{0}}L}{R}=\frac{1}{{{\omega }_{0}}CR}\] Q is an indicator of the sharpness of the resonance. The higher the value of Q, the sharper is the peak value of current. Or Given, \[\phi =5{{t}^{2}}+6t+2\,mWb\] (i) Induced emf, \[e=\frac{d\phi }{dt}=(10t+6)\times {{10}^{-3}}Wb\] At \[t=1s,\] \[e=(10\times 1+6)\times {{10}^{-3}}=1.6\times {{10}^{-2}}V=16mV\] (ii) The direction of induced current is such as to oppose the change in flux. So, the direction of induced current flows through the resistor R from left to right. 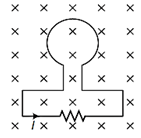
You need to login to perform this action.
You will be redirected in
3 sec
