| Double convex lens are to be manufactured from a glass of refractive index 1.5, with both faces of the same radius of curvature. What is the radius of curvature required, if the focal length is to be 30 cm? |
| Or |
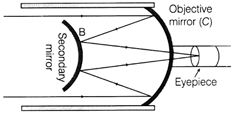
| A Cassegrain telescope uses two mirrors as shown in figure below. Such a telescope is built with the mirrors 20 mm apart. If the radius of curvature of the large mirror is 220 mm and of the small mirror is 140 mm, then where will the final image of an object at infinity be? |
Answer:
33 cm Or At a distance of 31.5 cm from the smaller mirror behind the bigger mirror. Given, the refractive index of glass with respect to air \[\,{{\,}^{a}}{{\mu }_{g}}=1.55\] 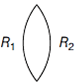 (\[\therefore \]both faces have same radius of curvature) For double convex lenses, \[{{R}_{1}}=R,\] \[{{R}_{2}}=-R\] Focal length of lens, \[\text{f}=+\,30\,cm\] Using lens maker?s formula, \[\frac{1}{\text{f}}=({{\,}^{a}}{{\mu }_{g}}-1)\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\] \[\Rightarrow \]\[\frac{1}{30}=(1.55-1)\left( \frac{1}{R}+\frac{1}{R} \right)\Rightarrow \frac{1}{30}=0.55\times \frac{2}{R}\] \[R=0.55\times 2\times 30=33\,cm\] This is the required radius of curvature. Or Given, radius of curvature of objective mirror \[{{R}_{1}}=220\,mm\] Radius of curvature of secondary mirror \[{{R}_{2}}=140\,mm\] \[{{\text{f}}_{2}}={{R}_{2}}/2=70\,mm\] Distance between the two mirrors d = 20 mm from objective mirror For secondary mirror, \[u={{\text{f}}_{1}}-d=110-20\,mm\] \[\frac{1}{\text{v}}=\frac{1}{{{\text{f}}_{2}}}-\frac{1}{u}=\frac{1}{70}-\frac{1}{90}\] \[\Rightarrow \] \[\text{v}\,\,\text{=}\,\,\text{315}\,\text{mm}\,\,\text{=}\,\,\text{31}\text{.5}\,\text{cm}\] \[\therefore \] The final image is at 31.5 cm to the right of secondary mirror.
(\[\therefore \]both faces have same radius of curvature) For double convex lenses, \[{{R}_{1}}=R,\] \[{{R}_{2}}=-R\] Focal length of lens, \[\text{f}=+\,30\,cm\] Using lens maker?s formula, \[\frac{1}{\text{f}}=({{\,}^{a}}{{\mu }_{g}}-1)\left( \frac{1}{{{R}_{1}}}-\frac{1}{{{R}_{2}}} \right)\] \[\Rightarrow \]\[\frac{1}{30}=(1.55-1)\left( \frac{1}{R}+\frac{1}{R} \right)\Rightarrow \frac{1}{30}=0.55\times \frac{2}{R}\] \[R=0.55\times 2\times 30=33\,cm\] This is the required radius of curvature. Or Given, radius of curvature of objective mirror \[{{R}_{1}}=220\,mm\] Radius of curvature of secondary mirror \[{{R}_{2}}=140\,mm\] \[{{\text{f}}_{2}}={{R}_{2}}/2=70\,mm\] Distance between the two mirrors d = 20 mm from objective mirror For secondary mirror, \[u={{\text{f}}_{1}}-d=110-20\,mm\] \[\frac{1}{\text{v}}=\frac{1}{{{\text{f}}_{2}}}-\frac{1}{u}=\frac{1}{70}-\frac{1}{90}\] \[\Rightarrow \] \[\text{v}\,\,\text{=}\,\,\text{315}\,\text{mm}\,\,\text{=}\,\,\text{31}\text{.5}\,\text{cm}\] \[\therefore \] The final image is at 31.5 cm to the right of secondary mirror.
You need to login to perform this action.
You will be redirected in
3 sec
