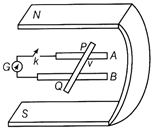
 A galvanometer G connects the rails through a switch k. Length of the rod is I and magnetic field is B, resistance of the closed loop containing the rod is R. Assume the field to be uniform.
A galvanometer G connects the rails through a switch k. Length of the rod is I and magnetic field is B, resistance of the closed loop containing the rod is R. Assume the field to be uniform. | (i) Suppose, k is open and the rod moves with a speed v in the direction shown. Give the polarity and magnitude of the induced emf. |
| (ii) What is the retarding force on the rod, when k is closed? |
| (iii) How much power is required (by an external agent) to keep the rod moving at the same speed v when k is closed? |
| (iv) How much power is dissipated as heat in the closed circuit? What is the source of the power? |
| Or |
| What are eddy currents? How are these produced? In what sense are eddy current undesirable in a transformer and how are these reduced in such a device? |
| An induced emf has no direction of its own. Comment. |
Answer:
(i) The magnitude of induced emf is \[e=Bl\text{v}\,\,\text{sin}\theta \] where, \[\theta \] is the angle between the rod PQ and field B According to Fleming?s left hand rule, the direction of current is perpendicular to direction of motion of conductor and direction of magnetic field i.e. in the direction from Q to P in the given diagram. That means electrons move from P to Q. So, there is an excess of electrons at Q which makes it negative and P is at positive potential. (ii) Retarding force on the rod is given by \[F=IlB\Rightarrow I=e/R\] \[\therefore \] \[F=elB/Rs\] (iii) Power required by external agent to keep the rod moving is \[P=F\times \text{v=}\frac{elB\text{v}}{R}\] (iv) Power dissipated as heat \[={{I}^{2}}R=\frac{{{e}^{2}}}{{{R}^{2}}}\times R=\frac{{{e}^{2}}}{R}\] The source of this power is the external agent. Or Eddy Current. The currents induced in bulk pieces of conductors, when the magnetic flux linked with the conductor changes, are known as eddy currents. Eddy currents are always produced in a plane perpendicular to the direction of magnetic field. Eddy current shows both heating and magnetic effects. The magnitude of eddy current is given by \[i=\frac{\text{Induced}\,\,\text{emf}}{\text{Resistance}}=\frac{e}{R}\] According to Faraday?s law, \[e=-\frac{d\phi }{dt},\] \[i=-\frac{d\phi /dt}{R}\] The direction of eddy currents can be given by Lenz?s law or by Fleming?s right hand rule. However, their flow patterns resemble swirling eddies in water. That is why, they are called eddy currents. These were discovered by Foucault in the year 1895 and hence, they are also named as Foucault current. e.g. When we move a metal plate out of a magnetic field, the relative motion of the field and the conductor again induces a current in the conductor. The conduction electrons build up the induced current whirl around within the plate as, if they were caught in an eddy of water. This is called the eddy current. Undesirable Effects of Eddy Currents Eddy currents are produced inside the iron cores of the rotating armatures of electric motors and dynamos and also in the cores of transformers, which experience flux changes, when they are in use. Eddy currents cause unnecessary heating and wastage of power. The heat produced by eddy currents may even damage the insulation of coils. Eddy currents are minimised by using laminations of metal to make a metal core. The laminations are separated by an insulating material. The plane of the laminations must be arranged parallel to the magnetic field, so that they cut across the eddy current paths. This arrangement reduces the strength of eddy currents. An induced emf has no direction of its own. Its direction is such that it opposes the change in magnetic flux.
You need to login to perform this action.
You will be redirected in
3 sec
