| A network of six identical capacitors, each of capacitance C is made in figure. Find the equivalent capacitance between the points A and B. |
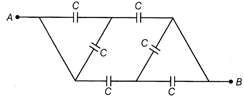
|
| Network of six identical capacitors |
Answer:
The capacitors can be rearranged as shown below.  Simplified circuit diagram of capacitors The equivalent capacitance is the resultant of parallel combination of two rows in which each row consists of 2C and C in series, i.e.
Simplified circuit diagram of capacitors The equivalent capacitance is the resultant of parallel combination of two rows in which each row consists of 2C and C in series, i.e. 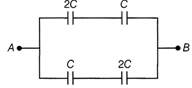 Simplified arranged capacitors Here, 2C and C are in series. So, their equivalent capacitance is \[\frac{1}{{{C}_{1}}}=\frac{1}{2C}+\frac{1}{C}\] \[\left[ \because \frac{1}{{{C}_{S}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}} \right]\] \[=\frac{3}{2C}\] \[\therefore \] \[{{C}_{1}}=\frac{2C}{3}\] Similarly, \[{{C}_{2}}=\frac{2C}{3}\] Now, \[\frac{2C}{3}\] and \[\frac{2C}{3}\] are in parallel. \[{{C}_{eq}}=\frac{2C}{3}+\frac{2C}{3}=\frac{4C}{3}F\] \[[\because {{C}_{P}}={{C}_{1}}+{{C}_{2}}]\] \[\therefore \] Equivalent capacitance between the points A and B is \[\frac{4C}{3}.\]
Simplified arranged capacitors Here, 2C and C are in series. So, their equivalent capacitance is \[\frac{1}{{{C}_{1}}}=\frac{1}{2C}+\frac{1}{C}\] \[\left[ \because \frac{1}{{{C}_{S}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}} \right]\] \[=\frac{3}{2C}\] \[\therefore \] \[{{C}_{1}}=\frac{2C}{3}\] Similarly, \[{{C}_{2}}=\frac{2C}{3}\] Now, \[\frac{2C}{3}\] and \[\frac{2C}{3}\] are in parallel. \[{{C}_{eq}}=\frac{2C}{3}+\frac{2C}{3}=\frac{4C}{3}F\] \[[\because {{C}_{P}}={{C}_{1}}+{{C}_{2}}]\] \[\therefore \] Equivalent capacitance between the points A and B is \[\frac{4C}{3}.\]
You need to login to perform this action.
You will be redirected in
3 sec
