question_answer

(i) light passes through two polaroids \[{{P}_{1}}\] and \[{{P}_{2}}\]  with pass axis of \[{{P}_{2}}\] making an angle, \[\theta \] with the pass axis of \[{{P}_{1}}.\] For what value of \[\theta \] is the intensity of emergent light zero?

(ii) A third polaroid is placed between \[{{P}_{1}}\] and \[{{P}_{2}}\] with its pass axis making an angle, \[\beta \] with the pass axis of \[{{P}_{1}}.\] Find the value of \[\beta \] for which the intensity of light from \[{{P}_{2}}\] is \[\frac{{{I}_{0}}}{8},\] where \[{{I}_{0}}\] is the intensity of light on the Polaroid \[{{P}_{1}}.\]

 

Answer:

            (i) By law of Malus, intensity of emergent light from \[{{P}_{2}}\] is \[I={{I}_{0}}{{\cos }^{2}}\theta ,\] where \[\theta \] is the angle between \[{{P}_{1}}\] and \[{{P}_{2}}.\] When \[\theta =90{}^\circ \Rightarrow I={{I}_{0}}\times 0\]        \[[\because \cos \theta =0]\] \[\therefore \] Intensity of emergent light, I = 0 (ii) Intensity of light from \[{{P}_{3}}\]             \[{{I}_{3}}=\left( \frac{{{I}_{0}}}{2}{{\cos }^{2}}\beta  \right)[co{{s}^{2}}(90{}^\circ -\beta )]\] 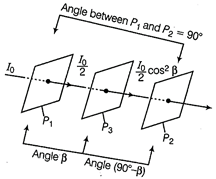            Light passes through polaroids Similarly, intensity of light from \[{{P}_{2}},\]             \[{{I}_{2}}=\frac{{{I}_{0}}}{2}{{\cos }^{2}}\beta {{\sin }^{2}}\beta =\frac{{{I}_{0}}}{8}{{\sin }^{2}}2\beta \] As,        \[\frac{{{I}_{0}}}{8}{{\sin }^{2}}2\beta =\frac{{{I}_{0}}}{8}\]          [given] So,       \[{{(\sin 2\beta )}^{2}}=1\] \[\Rightarrow \]   \[2\beta =90{}^\circ \]   \[\Rightarrow \]   \[\beta =45{}^\circ \]