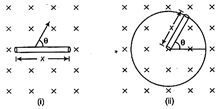
| Calculate the rate at which the flux linked with the generated area changes with time when a rod of length x is |
| (i) translated |
| (ii) rotated in a uniform field of induction B as shown in figure. |
|
| Or |
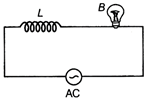
| An inductor, L of reactance, \[{{X}_{L}}\] is connected in series with a bulb B to an AC source as shown in the figure. Briefly explain how does the brightness of the bulb change, when |
|
| AC source |
| (i) number of turns of the inductor is reduced |
| (ii) a capacitor of reactance, \[{{X}_{C}}={{X}_{L}}\] is included in series in the same circuit? |
Answer:
(i) Component of velocity perpendicular to the rod \[=v\sin \theta .\] Therefore, in time t, area transversed (A) is, \[=x\times v\sin \theta \times t\] Since, \[\phi =B\cdot \,\,A=BA\cos \theta \] Here, \[\theta =0{}^\circ \] \[\therefore \] \[\phi =B(x\times v\sin \theta \times t)\cos 0{}^\circ =Bxvt\sin \theta \] Also, \[e=\frac{d\phi }{dt}=Bxv\sin \theta \] (ii) In time t, if \[\theta \] is the angle traced by the free end, then \[\therefore \] Area swept, \[A=\pi {{x}^{2}}\times \left( \frac{\theta }{2\pi } \right)=\frac{1}{2}{{x}^{2}}\theta \] Also, \[\phi =B\left( \frac{1}{2}{{x}^{2}}\theta \right)\cos 0{}^\circ =\frac{1}{2}B{{x}^{2}}\theta \] \[\therefore \] \[e=\frac{d\phi }{dt}\] \[=\frac{1}{2}B{{x}^{2}}\frac{d\theta }{dt}=\frac{1}{2}B{{x}^{2}}\omega \] Or (i) When the number of turns of the inductor is reduced, its inductance, L decreases. A decrease in inductance causes \[{{X}_{L}}\] to decrease and hence current in the circuit increases therefore brightness of the bulb increases. (ii) When the capacitor is connected in series in the circuit, then its impedance is given by \[Z=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}\] Here, \[{{X}_{L}}={{X}_{C}}\] \[\therefore \] Z = R Thus, impedance of the circuit becomes minimum and is equal to the resistance and hence, the brightness of the bulb increases to maximum.\
You need to login to perform this action.
You will be redirected in
3 sec
