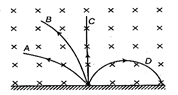
| A neutron, a proton, an electron and an\[\alpha \text{-particle}\] enter in a region of uniform magnetic field with equal velocities. The magnetic field is directed to the plane of paper. The tracks of the particles are shown in figure. Relate the tracks to particle. |
|
Answer:
As we know that force on a charged particle in a magnetic field is given by \[|F|\,\,=q|v\times B|\] or \[F=qvB\sin \theta \] (i) Track C corresponds to neutron, since neutron is a neutral particle, i.e., q = 0, Hence, it will be undeflected. (ii) For negatively charged particles i.e., electron, track D corresponds to electron by Fleming's left hand rule, it will be towards right. (iii) For positively charged particles, the direction of force, according to Fleming's left hand rule will be towards left, so proton and a-particles both will move towards left. Since, we know that, r = mv/Bq \[\Rightarrow \] \[r\propto (m/q)\] Also \[\frac{{{r}_{p}}}{{{r}_{\alpha }}}=\frac{{{m}_{p}}}{{{m}_{\alpha }}}\times \frac{{{q}_{\alpha }}}{{{q}_{p}}}=\left( \frac{m}{4m} \right)\times \left( \frac{2e}{e} \right)=\frac{1}{2}\] or \[{{r}_{\alpha }}=2{{r}_{p}}\] Hence, \[{{r}_{\alpha }}>{{r}_{p}}\] \[[\because {{q}_{\alpha }}=2{{q}_{p}}]\] So, track B corresponds to a-particle and track A to proton.
You need to login to perform this action.
You will be redirected in
3 sec
