| An inductor L, a capacitor C and a resistor R are connected in series in an AC circuit. Deduce with the help of suitable phasor diagram, a mathematical expression for impedance of this circuit. What is meant by resonance of this circuit? Prove that this circuit exhibits resonance at a frequency given by \[1/2\pi \sqrt{LC}.\] |
| OR |
| (i) A series L-C-R circuit is connected to an AC source of voltage V and angular frequency co when only the capacitor is removed, the current lags behind the voltage by a phase angle \['\phi '\] and when only the inductor is removed, the current leads the voltage by the same phase angle. Find the current flowing and the average power dissipated in the L-C-R circuit. |
| (ii) An alternating voltage given by V=140 sin 314t is connected across a pure resistor of resistance 50 Q. Find (a) the frequency of the source (b) the rms current through the resistor. |
Answer:
Let an alternating voltage \[V={{V}_{0}}\sin \omega t\] is applied across the series combination of L, C and R as shown in figure below.
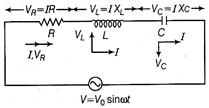 L-C-R circuit Since, I and \[{{V}_{R}}\] are in same phase, \[{{V}_{L}}\] leads I by phase \[\pi /2\] and \[{{V}_{C}}\] lags I by phase \[\pi /2.\]and So, \[{{V}_{L}}\] and \[{{V}_{C}}\] are in opposite phase and their resultant is \[({{V}_{L}}-{{V}_{C}}).\] The phasor diagram is shown below,
L-C-R circuit Since, I and \[{{V}_{R}}\] are in same phase, \[{{V}_{L}}\] leads I by phase \[\pi /2\] and \[{{V}_{C}}\] lags I by phase \[\pi /2.\]and So, \[{{V}_{L}}\] and \[{{V}_{C}}\] are in opposite phase and their resultant is \[({{V}_{L}}-{{V}_{C}}).\] The phasor diagram is shown below,
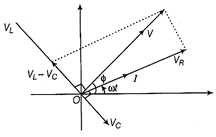 The resultant of \[{{V}_{L}}\] and \[{{V}_{C}}\] i.e. \[{{V}_{L}}-{{V}_{C}}\] and \[{{V}_{R}}\] must be equal to the applied voltage, given by the diagonal the parallelogram. By Pythagoras theorem, \[{{V}^{2}}=V_{R}^{2}+{{({{V}_{L}}-{{V}_{C}})}^{2}}\] But \[{{V}_{R}}=IR,\] \[{{V}_{L}}=I{{X}_{L}},\] \[{{V}_{C}}=I\,\,{{X}_{C}}\] where, \[{{X}_{L}}=\omega L\] = inductive reactance \[{{X}_{C}}=\frac{1}{\omega C}\] = capacitive reactance \[\therefore \] \[{{V}^{2}}={{(IR)}^{2}}+{{(I\,\,{{X}_{L}}-I\,\,{{X}_{C}})}^{2}}\] or, \[\frac{{{V}^{2}}}{{{I}^{2}}}={{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}\] or, \[\frac{V}{I}=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}\] where, V and I are instantaneous voltage and current and V/I gives the net opposition offered by circuit which is known as impedance (Z) of circuit. \[\therefore \] \[Z=\sqrt{{{R}^{2}}+{{({{V}_{L}}-{{X}_{C}})}^{2}}}\] Resonance The series L-C-R circuit is said to be in resonance when the current through the circuit becomes maximum and inductive reactance becomes equal to the capacitance reactance i.e. \[\therefore \] \[{{X}_{L}}={{X}_{C}}\] or \[\omega L=\frac{1}{\omega C}\] or, \[{{\omega }^{2}}=\frac{1}{LC}\] \[\Rightarrow \] \[\omega =\frac{1}{\sqrt{LC}}\Rightarrow 2\pi f=\frac{1}{\sqrt{LC}}\] where, f is resonant frequency, \[f=\frac{1}{2\pi \sqrt{LC}}\] Hence proved. Or (i) As we know that, \[\tan \phi =\frac{{{X}_{L}}-{{X}_{C}}}{R}=\frac{\omega L-\frac{1}{\omega C}}{R}\] Now, when capacitor is removed, \[\tan \phi =\frac{\omega L}{R}\] and when inductor is removed, \[\tan \phi =\frac{\omega C}{R}\] Negative sign indicates that current leads the voltage. \[\therefore \] \[\omega L=1/\omega C\Rightarrow \omega =1\sqrt{LC}\] \[\Rightarrow L\text{-}C\text{-}R\] circuit is in resonance. \[\therefore \] \[{{i}_{rms}}={{V}_{eff}}/R=V/R\] \[{{P}_{av}}={{V}_{rms}}{{i}_{rms}}={{V}^{2}}_{rms}/R=\frac{{{V}^{2}}}{R}\] (ii) Given, \[V=140\sin 314t,\] \[R=50\Omega \] Comparing it with \[V={{V}_{0}}\sin \omega t\] (a) Here, \[\omega =314rad/s\] i.e. \[2\pi v=314\] \[[\because \omega =2\pi v]\] \[\Rightarrow \] \[v=\frac{314}{2\pi }=\frac{31400}{2\times .314}=50Hz\] Frequency of AC, v = 50Hz (b) As, \[{{I}_{rms}}=\frac{{{V}_{rms}}}{R}\] and \[{{V}_{rms}}=\frac{{{V}_{0}}}{\sqrt{2}}\] Here, \[{{V}_{0}}=140V\] \[\Rightarrow \] \[{{V}_{rms}}=\frac{140}{\sqrt{2}}=70\sqrt{2}V\] \[\therefore \] \[{{I}_{rms}}=\frac{70\sqrt{2}}{R}=\frac{70\sqrt{2}}{50}=1.9A\] or 2A
The resultant of \[{{V}_{L}}\] and \[{{V}_{C}}\] i.e. \[{{V}_{L}}-{{V}_{C}}\] and \[{{V}_{R}}\] must be equal to the applied voltage, given by the diagonal the parallelogram. By Pythagoras theorem, \[{{V}^{2}}=V_{R}^{2}+{{({{V}_{L}}-{{V}_{C}})}^{2}}\] But \[{{V}_{R}}=IR,\] \[{{V}_{L}}=I{{X}_{L}},\] \[{{V}_{C}}=I\,\,{{X}_{C}}\] where, \[{{X}_{L}}=\omega L\] = inductive reactance \[{{X}_{C}}=\frac{1}{\omega C}\] = capacitive reactance \[\therefore \] \[{{V}^{2}}={{(IR)}^{2}}+{{(I\,\,{{X}_{L}}-I\,\,{{X}_{C}})}^{2}}\] or, \[\frac{{{V}^{2}}}{{{I}^{2}}}={{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}\] or, \[\frac{V}{I}=\sqrt{{{R}^{2}}+{{({{X}_{L}}-{{X}_{C}})}^{2}}}\] where, V and I are instantaneous voltage and current and V/I gives the net opposition offered by circuit which is known as impedance (Z) of circuit. \[\therefore \] \[Z=\sqrt{{{R}^{2}}+{{({{V}_{L}}-{{X}_{C}})}^{2}}}\] Resonance The series L-C-R circuit is said to be in resonance when the current through the circuit becomes maximum and inductive reactance becomes equal to the capacitance reactance i.e. \[\therefore \] \[{{X}_{L}}={{X}_{C}}\] or \[\omega L=\frac{1}{\omega C}\] or, \[{{\omega }^{2}}=\frac{1}{LC}\] \[\Rightarrow \] \[\omega =\frac{1}{\sqrt{LC}}\Rightarrow 2\pi f=\frac{1}{\sqrt{LC}}\] where, f is resonant frequency, \[f=\frac{1}{2\pi \sqrt{LC}}\] Hence proved. Or (i) As we know that, \[\tan \phi =\frac{{{X}_{L}}-{{X}_{C}}}{R}=\frac{\omega L-\frac{1}{\omega C}}{R}\] Now, when capacitor is removed, \[\tan \phi =\frac{\omega L}{R}\] and when inductor is removed, \[\tan \phi =\frac{\omega C}{R}\] Negative sign indicates that current leads the voltage. \[\therefore \] \[\omega L=1/\omega C\Rightarrow \omega =1\sqrt{LC}\] \[\Rightarrow L\text{-}C\text{-}R\] circuit is in resonance. \[\therefore \] \[{{i}_{rms}}={{V}_{eff}}/R=V/R\] \[{{P}_{av}}={{V}_{rms}}{{i}_{rms}}={{V}^{2}}_{rms}/R=\frac{{{V}^{2}}}{R}\] (ii) Given, \[V=140\sin 314t,\] \[R=50\Omega \] Comparing it with \[V={{V}_{0}}\sin \omega t\] (a) Here, \[\omega =314rad/s\] i.e. \[2\pi v=314\] \[[\because \omega =2\pi v]\] \[\Rightarrow \] \[v=\frac{314}{2\pi }=\frac{31400}{2\times .314}=50Hz\] Frequency of AC, v = 50Hz (b) As, \[{{I}_{rms}}=\frac{{{V}_{rms}}}{R}\] and \[{{V}_{rms}}=\frac{{{V}_{0}}}{\sqrt{2}}\] Here, \[{{V}_{0}}=140V\] \[\Rightarrow \] \[{{V}_{rms}}=\frac{140}{\sqrt{2}}=70\sqrt{2}V\] \[\therefore \] \[{{I}_{rms}}=\frac{70\sqrt{2}}{R}=\frac{70\sqrt{2}}{50}=1.9A\] or 2A
You need to login to perform this action.
You will be redirected in
3 sec
