| (i) How does an unpolarised light incident on a polaroid get polarised? Describe briefly with the help of necessary diagram, the polarisation of light by reflection from a transparent medium. |
| (ii) Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them, so that the intensity of polarised light transmitted by polaroid B reduces to 1/8 the of the intensity of unpolarised light incident on A? |
| OR |
| A compound microscope consists of an objective lens of focal length 2,0 cm and an eye piece of focal length 6.25 cm separated by a distance of 15 cm. How far from the objective lens should an object be placed in order to obtain the final image |
| (i) At least distance of distinct vision \[(D=25cm)\] |
| (ii) At infinity What is the magnifying power in each case? |
Answer:
(i) Polarisation of Light If a transverse mechanical wave is passed through a narrow slit, so that the plane of vibration of the wave is parallel to the slit, then the wave passes through the slit with its vibrations being unaffected and the wave is said to be plane polarised. 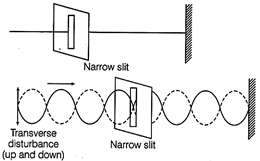 Polarisation of transverse wave Polarisation of Light by Reflection When an unpolarised light is incident on the boundary between two transparent media, the reflected light is polarised with its electric field vector perpendicular to the plane of incidence when the reflected and refracted rays make a right angle with each other. Thus, when reflected wave is perpendicular to the refracted wave, the reflected wave is a totally polarised wave. The angle of incidence in this case is called Brewster's angle \[{{i}_{B}}.\] Since, \[{{i}_{B}}+r=\frac{\pi }{2}\] From Snell's law, \[\mu =\frac{\sin {{i}_{B}}}{\sin \,r}=\frac{\sin {{i}_{B}}}{\sin \left( \frac{\pi }{2}-{{i}_{B}} \right)}=\frac{\sin {{i}_{B}}}{\cos {{i}_{B}}}=\tan {{i}_{B}}\] \[\therefore \] \[\mu =\tan {{i}_{B}}\] This is Brewster's law. If QR and QS are the reflected and the refracted rays respectively, \[{{i}_{B}}\] is the angle of incidence and r is the angle of refraction.
Polarisation of transverse wave Polarisation of Light by Reflection When an unpolarised light is incident on the boundary between two transparent media, the reflected light is polarised with its electric field vector perpendicular to the plane of incidence when the reflected and refracted rays make a right angle with each other. Thus, when reflected wave is perpendicular to the refracted wave, the reflected wave is a totally polarised wave. The angle of incidence in this case is called Brewster's angle \[{{i}_{B}}.\] Since, \[{{i}_{B}}+r=\frac{\pi }{2}\] From Snell's law, \[\mu =\frac{\sin {{i}_{B}}}{\sin \,r}=\frac{\sin {{i}_{B}}}{\sin \left( \frac{\pi }{2}-{{i}_{B}} \right)}=\frac{\sin {{i}_{B}}}{\cos {{i}_{B}}}=\tan {{i}_{B}}\] \[\therefore \] \[\mu =\tan {{i}_{B}}\] This is Brewster's law. If QR and QS are the reflected and the refracted rays respectively, \[{{i}_{B}}\] is the angle of incidence and r is the angle of refraction. 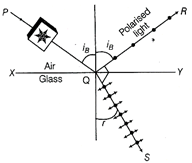 Polarisation by reflection (ii) Let 9 be the angle between the pass axis A and C. Intensity of light passing through \[A=\frac{{{l}_{0}}}{2}\] Intensity of light passing through \[C=\frac{{{l}_{0}}}{2}{{\cos }^{2}}\theta \] Intensity of light passing through B \[=\left( \frac{{{l}_{0}}}{2}{{\cos }^{2}}\theta \right)\cdot {{\cos }^{2}}(90{}^\circ -\theta )\] \[=\frac{{{l}_{0}}}{2}{{(\sin \theta \cdot cos\theta )}^{2}}\] But, \[\frac{{{l}_{0}}}{2}{{(\sin \theta \cdot \cos \theta )}^{2}}=\frac{{{l}_{0}}}{8}\] According to problem, \[{{(\sin \theta \cos \theta )}^{2}}=\frac{1}{4}\] \[\therefore \] \[{{\left( \frac{\sin 2\theta }{2} \right)}^{2}}=\frac{1}{4}\Rightarrow \frac{\sin 2\theta }{2}=\frac{1}{4}\] or \[\sin 2\theta =1\] \[\Rightarrow \] \[2\theta =90{}^\circ \Rightarrow \theta =45{}^\circ \] Or (i) For the compound microscope, \[{{f}_{0}}=2cm,\] \[{{f}_{e}}=6.25cm,\] \[L=15cm\] \[D=25cm\] Image distance, \[{{v}_{e}}=-25cm\] \[\therefore \] \[\frac{1}{{{v}_{e}}}-\frac{1}{{{u}_{e}}}=\frac{1}{{{f}_{e}}}\Rightarrow \frac{1}{{{u}_{e}}}=\frac{1}{{{v}_{e}}}-\frac{1}{{{f}_{e}}}\] \[=\frac{1}{-25}-\frac{1}{6.25}=\frac{-1}{5}\] \[\therefore \] \[{{u}_{e}}=-5cm,\] \[L=15cm\] \[\therefore \] Distance of image from objective, \[{{v}_{o}}=15-5=10cm\] \[\frac{1}{{{u}_{o}}}=\frac{1}{{{v}_{o}}}-\frac{1}{{{f}_{o}}}=\frac{1}{10}-\frac{1}{2}=\frac{-2}{5}\] Distance of object from objective lens, \[{{u}_{o}}=\frac{-5}{2}=-2.5cm\] \[\therefore \] Magnifying power, \[m={{m}_{o}}\times {{m}_{e}}=\frac{{{v}_{o}}}{{{u}_{o}}}\left( 1+\frac{D}{{{f}_{e}}} \right)\] \[=\frac{10}{2.5}\left( 1+\frac{25}{6.25} \right)=20\] (ii) \[{{v}_{e}}=\infty ,\] \[{{f}_{e}}=6.25cm\] \[\therefore \] \[\frac{1}{\infty }-\frac{1}{{{u}_{e}}}=\frac{1}{-\,6.25}\] \[{{u}_{e}}=6.25cm\] \[{{v}_{o}}=15-6.25=8.75cm\] \[\therefore \] \[\frac{1}{{{u}_{o}}}=\frac{1}{{{v}_{o}}}-\frac{1}{{{f}_{o}}}=\frac{1}{8.75}-\frac{1}{2}=\frac{-1}{2.59}\] \[\therefore \] \[{{u}_{o}}=-2.59cm\] The distance of object from objective lens \[=2.59cm\] Magnifying power, \[m={{m}_{o}}\times {{m}_{e}}=\frac{{{v}_{o}}}{{{u}_{o}}}.\frac{D}{{{f}_{e}}}\] \[=\frac{8.75}{2.59}\times \frac{25}{6.25}=13.5\]
Polarisation by reflection (ii) Let 9 be the angle between the pass axis A and C. Intensity of light passing through \[A=\frac{{{l}_{0}}}{2}\] Intensity of light passing through \[C=\frac{{{l}_{0}}}{2}{{\cos }^{2}}\theta \] Intensity of light passing through B \[=\left( \frac{{{l}_{0}}}{2}{{\cos }^{2}}\theta \right)\cdot {{\cos }^{2}}(90{}^\circ -\theta )\] \[=\frac{{{l}_{0}}}{2}{{(\sin \theta \cdot cos\theta )}^{2}}\] But, \[\frac{{{l}_{0}}}{2}{{(\sin \theta \cdot \cos \theta )}^{2}}=\frac{{{l}_{0}}}{8}\] According to problem, \[{{(\sin \theta \cos \theta )}^{2}}=\frac{1}{4}\] \[\therefore \] \[{{\left( \frac{\sin 2\theta }{2} \right)}^{2}}=\frac{1}{4}\Rightarrow \frac{\sin 2\theta }{2}=\frac{1}{4}\] or \[\sin 2\theta =1\] \[\Rightarrow \] \[2\theta =90{}^\circ \Rightarrow \theta =45{}^\circ \] Or (i) For the compound microscope, \[{{f}_{0}}=2cm,\] \[{{f}_{e}}=6.25cm,\] \[L=15cm\] \[D=25cm\] Image distance, \[{{v}_{e}}=-25cm\] \[\therefore \] \[\frac{1}{{{v}_{e}}}-\frac{1}{{{u}_{e}}}=\frac{1}{{{f}_{e}}}\Rightarrow \frac{1}{{{u}_{e}}}=\frac{1}{{{v}_{e}}}-\frac{1}{{{f}_{e}}}\] \[=\frac{1}{-25}-\frac{1}{6.25}=\frac{-1}{5}\] \[\therefore \] \[{{u}_{e}}=-5cm,\] \[L=15cm\] \[\therefore \] Distance of image from objective, \[{{v}_{o}}=15-5=10cm\] \[\frac{1}{{{u}_{o}}}=\frac{1}{{{v}_{o}}}-\frac{1}{{{f}_{o}}}=\frac{1}{10}-\frac{1}{2}=\frac{-2}{5}\] Distance of object from objective lens, \[{{u}_{o}}=\frac{-5}{2}=-2.5cm\] \[\therefore \] Magnifying power, \[m={{m}_{o}}\times {{m}_{e}}=\frac{{{v}_{o}}}{{{u}_{o}}}\left( 1+\frac{D}{{{f}_{e}}} \right)\] \[=\frac{10}{2.5}\left( 1+\frac{25}{6.25} \right)=20\] (ii) \[{{v}_{e}}=\infty ,\] \[{{f}_{e}}=6.25cm\] \[\therefore \] \[\frac{1}{\infty }-\frac{1}{{{u}_{e}}}=\frac{1}{-\,6.25}\] \[{{u}_{e}}=6.25cm\] \[{{v}_{o}}=15-6.25=8.75cm\] \[\therefore \] \[\frac{1}{{{u}_{o}}}=\frac{1}{{{v}_{o}}}-\frac{1}{{{f}_{o}}}=\frac{1}{8.75}-\frac{1}{2}=\frac{-1}{2.59}\] \[\therefore \] \[{{u}_{o}}=-2.59cm\] The distance of object from objective lens \[=2.59cm\] Magnifying power, \[m={{m}_{o}}\times {{m}_{e}}=\frac{{{v}_{o}}}{{{u}_{o}}}.\frac{D}{{{f}_{e}}}\] \[=\frac{8.75}{2.59}\times \frac{25}{6.25}=13.5\]
You need to login to perform this action.
You will be redirected in
3 sec
