| Find an expression for the force acting per unit length between two straight parallel current carrying conductors and hence define one ampere current. |
| Or |
| In a given figure, a rectangular current carrying loop placed 2 cm away from a long, straight, current carrying conductor, What is the magnitude and direction of the net force acting on the loop? |
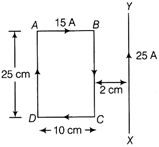
Answer:
Consider two straight and parallel current carrying long conductors separated by a distance, r and carrying currents, \[{{I}_{1}}\] and \[{{I}_{2}}\] in the same directions. 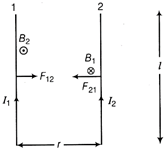 Two straight current carrying long conductors Magnetic field produced by the first conductor), distance, r (at the position of second conductor), \[{{B}_{1}}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}}{r}\] ?(i) (perpendicular to the plane of paper in downward direction) Force acting on length, l of second conductor, \[{{F}_{21}}={{B}_{1}}{{I}_{2}}l\sin 90{}^\circ \] Putting the value of \[{{B}_{1}}\] from Eq. (i), we get \[{{F}_{21}}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}l\] Force acting per unit length, \[\frac{{{F}_{21}}}{l}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}\] [towards first conductor] Similarly, we can find force acting per unit length on first wire. \[\frac{{{F}_{12}}}{l}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}\] [towards second conductor] Therefore, force acting per unit length of wires \[F=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}\] Definition of one ampere If two parallel straight conductors separated by a distance of one metre in vacuum carrying equal currents in the same direction and attracts each other with a force per unit length of \[2\times {{10}^{-7}}N{{m}^{-1}},\] then current in each conductor is said to be one ampere. Or Given, \[{{I}_{1}}=15A,\] \[{{I}_{2}}=25A\] \[{{r}_{1}}=2\times {{10}^{-2}}m,\] \[{{r}_{2}}=(2+10)\times {{10}^{-2}}m\] Force on BC, \[{{F}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{l}_{1}}{{l}_{2}}}{{{r}_{1}}}\times length\,\,BC\] \[=\frac{{{10}^{-7}}\times 2\times 15\times 25}{(2\times {{10}^{2}})}\times (25\times {{10}^{-2}})\] \[=9.375\times {{10}^{-4}}N\] (repulsive, away from xy) Force on DA, \[{{F}_{2}}\frac{{{\mu }_{0}}}{4\pi }\frac{2{{l}_{1}}{{l}_{2}}}{{{r}_{2}}}\times length\,DA\] \[=\frac{{{10}^{-7}}\times 2\times 15\times 25}{(2+10){{10}^{-2}}}\times 25\times {{10}^{-2}}=1.52625\times {{10}^{-4}}N\] (attractive towards XY) Net force on the loop \[F={{F}_{1}}-{{F}_{2}}=(9.375-1.5625)\times {{10}^{-4}}=7.8175\times {{10}^{-4}}\] (repulsive, away from XY)
Two straight current carrying long conductors Magnetic field produced by the first conductor), distance, r (at the position of second conductor), \[{{B}_{1}}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}}{r}\] ?(i) (perpendicular to the plane of paper in downward direction) Force acting on length, l of second conductor, \[{{F}_{21}}={{B}_{1}}{{I}_{2}}l\sin 90{}^\circ \] Putting the value of \[{{B}_{1}}\] from Eq. (i), we get \[{{F}_{21}}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}l\] Force acting per unit length, \[\frac{{{F}_{21}}}{l}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}\] [towards first conductor] Similarly, we can find force acting per unit length on first wire. \[\frac{{{F}_{12}}}{l}=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}\] [towards second conductor] Therefore, force acting per unit length of wires \[F=\frac{{{\mu }_{0}}}{2\pi }\frac{{{I}_{1}}{{I}_{2}}}{r}\] Definition of one ampere If two parallel straight conductors separated by a distance of one metre in vacuum carrying equal currents in the same direction and attracts each other with a force per unit length of \[2\times {{10}^{-7}}N{{m}^{-1}},\] then current in each conductor is said to be one ampere. Or Given, \[{{I}_{1}}=15A,\] \[{{I}_{2}}=25A\] \[{{r}_{1}}=2\times {{10}^{-2}}m,\] \[{{r}_{2}}=(2+10)\times {{10}^{-2}}m\] Force on BC, \[{{F}_{1}}=\frac{{{\mu }_{0}}}{4\pi }\frac{2{{l}_{1}}{{l}_{2}}}{{{r}_{1}}}\times length\,\,BC\] \[=\frac{{{10}^{-7}}\times 2\times 15\times 25}{(2\times {{10}^{2}})}\times (25\times {{10}^{-2}})\] \[=9.375\times {{10}^{-4}}N\] (repulsive, away from xy) Force on DA, \[{{F}_{2}}\frac{{{\mu }_{0}}}{4\pi }\frac{2{{l}_{1}}{{l}_{2}}}{{{r}_{2}}}\times length\,DA\] \[=\frac{{{10}^{-7}}\times 2\times 15\times 25}{(2+10){{10}^{-2}}}\times 25\times {{10}^{-2}}=1.52625\times {{10}^{-4}}N\] (attractive towards XY) Net force on the loop \[F={{F}_{1}}-{{F}_{2}}=(9.375-1.5625)\times {{10}^{-4}}=7.8175\times {{10}^{-4}}\] (repulsive, away from XY)
You need to login to perform this action.
You will be redirected in
3 sec
