| When a circuit element 'X' is connected across an AC source, a current of \[\sqrt{2}\] A flows through it and this current is in phase with the applied voltage. When another element' Y' is connected across the same AC source, the same current flows in the circuit but it leads the voltage by \[\pi /2\] radians. |
| (i) Name the element X and Y. |
| (ii) Find the current that flows in the circuit when series combination of X and Y is connected across the same voltage. |
| (iii) Plot a graph showing variation of the net impedance of this series combination of X and Y as a function of the angular frequency of the applied voltage. |
Answer:
(i) The circuit element X is a resistor and Visa capacitor. (ii) Here, \[R={{X}_{C}}=\frac{{{V}_{eff}}}{\sqrt{2}}\Omega \] When X and Y are connected in series, the impedance becomes \[Z=\sqrt{{{R}^{2}}+X_{C}^{2}}=\sqrt{2{{R}^{2}}}=\sqrt{2}R\] Current, \[{{I}_{eff}}=\frac{{{V}_{eff}}}{Z}=\frac{{{V}_{eff}}}{\sqrt{2}R}=\frac{\sqrt{2}R}{\sqrt{2}R}=1A\] (iii) Impedance \[Z=\sqrt{{{R}^{2}}+X_{C}^{2}}=\sqrt{{{R}^{2}}+\frac{1}{{{\omega }^{2}}{{C}^{2}}}}\] The \[Z\text{-}\omega \] graph will be of the type as shown in figure. 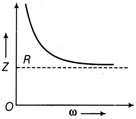
You need to login to perform this action.
You will be redirected in
3 sec
