| Find an expression for the torque acting on an electric dipole placed in uniform electric field. A system of two charges \[{{q}_{A}}=2.5\times {{10}^{-7}}C\] and \[{{q}_{B}}=-2.5\times {{10}^{-7}}C\] located at points \[A(0,0-15)cm\] and \[B(0,0,+15)\,cm,\] respectively. |
| Find the electric dipole moment of the system and the magnitude of the torque acting on it, when it is placed in a uniform electric field \[5\times {{10}^{4}}\,N{{C}^{-1}},\] making an angle of \[30{}^\circ ,\] with the Z-axis. |
| Or |
| A capacitor of capacitance C is charged fully by connecting it to a battery of emf E. It is then disconnected, from the battery. If the separation between the plates of the capacitor is now doubled, what will |
| (i) capacitance of the capacitor |
| (ii) charge stored by the capacitor |
| (iii) potential difference across it |
| (iv) field strength between the plates |
| (v) energy stored by the capacitor? |
Answer:
consider an electric dipole AB consists of two point charges +q and \[-\,q,\] separated by a distance 2a. It is placed in a uniform electric field E, making an angle, \[\theta .\] 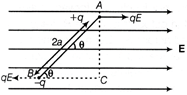 An electric dipole in a Uniform electric field Force acting on charge + q, \[{{F}_{1}}=qE\] [along the direction of E] Force acting on charge\[-q,\] \[{{F}_{2}}=qE\] [opposite to the direction of E] Forces \[{{F}_{1}}\] and \[{{F}_{2}}\] are equal in magnitude, opposite in direction having different lines of action of force. Therefore, it forms a couple of force. Torque acting on dipole = force \[\times \] Perpendicular distance between the forces From \[\Delta ACB,\] \[\tau =qE\times AC\] \[\sin \theta =AC/AB\] or \[AC=AB\sin \theta \] or \[AC=2a\sin \theta \] \[\therefore \] \[\tau =qE\times 2a\sin \,\,\theta \] But \[q\times 2a=p\] [electric dipole moment] \[\therefore \] \[\tau =pE\sin \theta \] \[\overrightarrow{\tau }=p\times E\] Here. Charge \[{{q}_{A}}={{q}_{B}}=2.5\times {{10}^{-7}}C\]
An electric dipole in a Uniform electric field Force acting on charge + q, \[{{F}_{1}}=qE\] [along the direction of E] Force acting on charge\[-q,\] \[{{F}_{2}}=qE\] [opposite to the direction of E] Forces \[{{F}_{1}}\] and \[{{F}_{2}}\] are equal in magnitude, opposite in direction having different lines of action of force. Therefore, it forms a couple of force. Torque acting on dipole = force \[\times \] Perpendicular distance between the forces From \[\Delta ACB,\] \[\tau =qE\times AC\] \[\sin \theta =AC/AB\] or \[AC=AB\sin \theta \] or \[AC=2a\sin \theta \] \[\therefore \] \[\tau =qE\times 2a\sin \,\,\theta \] But \[q\times 2a=p\] [electric dipole moment] \[\therefore \] \[\tau =pE\sin \theta \] \[\overrightarrow{\tau }=p\times E\] Here. Charge \[{{q}_{A}}={{q}_{B}}=2.5\times {{10}^{-7}}C\] 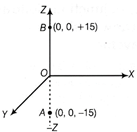 Geometrical representation of points A and B Length of dipole = 2a = 30 cm = 0.30 m \[\therefore \] Electric dipole moment (p) =q (2a) \[p=2.5\times {{10}^{-7}}\times 0.30=7.5\times {{10}^{-8}}C-m\] This dipole moment p is along the negative Z-axis. Also, uniform electric field, \[E=5\times {{10}^{4}}N{{C}^{-1}},\] at an angle of \[\theta =30{}^\circ \] with the Z-axis or p. \[\therefore \] Torque acting on electric dipole, \[\tau =pE\sin \theta \] \[=5\times {{10}^{4}}\times 7.5\times {{10}^{-8}}\times \sin 30{}^\circ \] \[=37.5\times {{10}^{-4}}\times 1/2\] \[=18.75\times {{10}^{-4}}\] \[=1.88\times {{10}^{-3}}N-m\] Or (i) Capacitance of the capacitor, \[C=\frac{KA{{\varepsilon }_{0}}}{d}\Rightarrow C\propto \frac{1}{d}\] When separation between the plates is doubled the capacitance is reduced to half of its initial value. (ii) Charge stored by the capacitor would remain unchanged. (iii) Potential difference between the plates, \[V=q/C\] As, capacitance of the capacitor \[(C=K\,A{{\varepsilon }_{0}}/d)\] reduces to half and hence potential difference between the plates becomes twice of the initial value i.e. 2 V. (iv) Field strength between the plates, E =V/d \[E=\frac{2V}{2d}=\frac{V}{d}\] [same] (v) Energy stored by the capacitor, \[U=\frac{1}{2}\frac{{{q}^{2}}}{C}\] As, capacitance reduces to half and charge remains same hence energy stored would be doubled.
Geometrical representation of points A and B Length of dipole = 2a = 30 cm = 0.30 m \[\therefore \] Electric dipole moment (p) =q (2a) \[p=2.5\times {{10}^{-7}}\times 0.30=7.5\times {{10}^{-8}}C-m\] This dipole moment p is along the negative Z-axis. Also, uniform electric field, \[E=5\times {{10}^{4}}N{{C}^{-1}},\] at an angle of \[\theta =30{}^\circ \] with the Z-axis or p. \[\therefore \] Torque acting on electric dipole, \[\tau =pE\sin \theta \] \[=5\times {{10}^{4}}\times 7.5\times {{10}^{-8}}\times \sin 30{}^\circ \] \[=37.5\times {{10}^{-4}}\times 1/2\] \[=18.75\times {{10}^{-4}}\] \[=1.88\times {{10}^{-3}}N-m\] Or (i) Capacitance of the capacitor, \[C=\frac{KA{{\varepsilon }_{0}}}{d}\Rightarrow C\propto \frac{1}{d}\] When separation between the plates is doubled the capacitance is reduced to half of its initial value. (ii) Charge stored by the capacitor would remain unchanged. (iii) Potential difference between the plates, \[V=q/C\] As, capacitance of the capacitor \[(C=K\,A{{\varepsilon }_{0}}/d)\] reduces to half and hence potential difference between the plates becomes twice of the initial value i.e. 2 V. (iv) Field strength between the plates, E =V/d \[E=\frac{2V}{2d}=\frac{V}{d}\] [same] (v) Energy stored by the capacitor, \[U=\frac{1}{2}\frac{{{q}^{2}}}{C}\] As, capacitance reduces to half and charge remains same hence energy stored would be doubled.
You need to login to perform this action.
You will be redirected in
3 sec
