Answer:
Let a rod PQ is horizontally placed on an inclined plane as shown in figure. 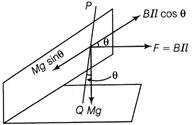 Inclined plane
Inclined plane
For rod to be stationary, \[Mg\,\sin \theta =BIl\cos \theta \] ?(i) If l is the length of rod and m as mass per unit length. i.e. \[\frac{M}{l}=m\] \[\Rightarrow \] M = ml \[\therefore \] \[(ml)\,g\,sin\theta =BIlcos\theta \] or \[I=\frac{mg\,\tan \theta }{B}=\frac{0.03\times 9.8\,\tan \,30{}^\circ }{0.15}\] \[\Rightarrow \] I = 1.132 A Forces act on the current carrying rod PQ are: (i) Weight (mg) (vertically downward) (1) (ii) Horizontal force, \[F=IBl\] (due to magnetic field B) Resolving mg and BIl along and perpendicular to inclined plane.
You need to login to perform this action.
You will be redirected in
3 sec
