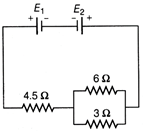
| Two cells \[{{E}_{1}}\] and \[{{E}_{2}}\]connected as shown in figure have an emf 5 V and 9 V and internal resistance of \[0.3\,\Omega ,\] and \[1.2\,\Omega \] respectively. Calculate |
| (i) the value of current flowing through If resistance of \[3\,\Omega .\] |
| (ii) power dissipated in the resistance of \[6\,\Omega .\] |
|
Answer:
(i) Here net emf of circuit \[E={{E}_{2}}-{{E}_{1}}=9-5=4\,V\] and total resistance of the circuit \[R=\frac{6\times 3}{6+3}+4.5+0.3+1.2=8\,\Omega \] \[\therefore \] Main circuit current \[I=E/R=4V/8\,\Omega =0.5\,A\] If current flowing through \[3\,\Omega \] resistance be \[{{I}_{1}},\] then current flowing through \[6\,\Omega \] resistance will be \[(0.5-{{I}_{1}})\] and hence \[3{{I}_{1}}=6\times (0.5-{{I}_{1}})\] \[\Rightarrow \] \[{{I}_{1}}=0.33\,A\] (ii) Now, current through \[6\,\Omega \] resistance is \[I{{'}_{1}}=0.5-{{I}_{1}}=0.5-0.33=0.17\,A\] \[\therefore \] Power dissipated in \[6\,\Omega \] resistance is \[P={{(I{{'}_{1}})}^{2}}\times 6={{(0.17)}^{2}}\times 6=0.173\,W\]
You need to login to perform this action.
You will be redirected in
3 sec
