| A series L-C-R circuit with L = 0.12 H, C = 480 nF, \[R\text{ }=\text{ }23\,\Omega \] is connected to a 230 V variable frequency supply. |
| (i) What is the source frequency for which current amplitude is maximum? Obtain this maximum value. |
| (ii) What is the source frequency for which average power absorbed by the circuit is maximum? Obtain the value of maximum power. |
| (iii) For which frequency of the source is the power transferred to the circuit half the power at resonant? |
| What is the current amplitude at these frequencies? What is the 0-factor of the given circuit? |
| Or |
| (i) State Faraday's laws of electromagnetic induction. |
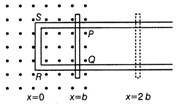
| (ii) Figure below shows a rectangular conductor PQRS in which the conductor PQ is free to move in a uniform magnetic field B perpendicular to the plane of paper. |
| The field extends from x = 0 to x = b and is zero for x > b, assume that only the arm PQ possesses resistance r. |
| When arm PQ is pulled outward from x = 0 to x = 2b and is then moved backward to x = 0 with constant speed v, obtain the expressions for the flux and the induced emf. Sketch the variations of these quantities with distance \[0\le x\le 2b.\] |
 |
Answer:
Given, L = 0.12 H, \[C=480\,nF=~480\times {{10}^{-9}}F\] \[R=23\,\Omega ,\]\[{{V}_{rms}}=230\,V,\] \[{{V}_{0}}=230\sqrt{2}V\] (i) Current amplitude, \[{{I}_{0}}=\frac{{{V}_{0}}}{\sqrt{{{R}^{2}}+{{\left( \omega L-\frac{1}{\omega C} \right)}^{2}}}}\] \[{{I}_{0}}\] would be maximum If, \[\omega ={{\omega }_{r}}=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{0.12}\times 480\times {{10}^{-9}}}\] \[=4166.7rad/s\] Source frequency, \[{{v}_{r}}=\frac{{{\omega }_{r}}}{2\pi }=\frac{4166.7}{2\pi }=663.48H\,z\] \[\therefore \] Maximum value of current, \[{{I}_{0}}=\frac{{{V}_{0}}}{R}=\frac{\sqrt{2}\times 230}{23}=14.14\,A\] (ii) Average power absorbed by the circuit is maximum if \[{{I}_{0}}={{I}_{0}}\] at \[\omega ={{\omega }_{r}}\] \[{{P}_{av}}=\frac{1}{2}I_{0}^{2}R=\frac{1}{2}{{(14.14)}^{2}}\times 23\] \[=2299.3\text{ }W\approx 2300\text{ }W\] (iii) Power transferred to circuit is half the power of resonant frequency, when \[\Delta \,\omega =\frac{R}{2L}=\frac{23}{2\times 0.12}=95.83rad/s\] \[\Delta v=\frac{\Delta \omega }{2\pi }=\frac{95.83}{2\pi }=15.2\,\,Hz\] \[\therefore \] Frequency when power transferred is half \[={{v}_{r}}+\Delta v=663.48\pm 15.2\] = 678.68 and 64828 Hz \[\therefore \] Current amplitude at these frequencies \[=\frac{{{I}_{0}}}{\sqrt{2}}=\frac{14.14}{1.414}=10\,A\] \[Q=\frac{{{\omega }_{r}}L}{R}=\frac{4166.7\times 0.12}{23}=21.74\] Or (i) Faraday's laws of electromagnetic induction (a) Whenever the magnetic flux linked with any loop or conductor changes, an emf is induced in it, which lasts, so long as change in magnetic flux in continuing. (b) The induced emf is directly proportional to the time rate of change of magnetic flux linked with the circuit. \[\therefore \] \[e\propto \frac{-d\phi }{dt}\] The negative sign shows that the induced emf opposes the change in magnetic flux. (ii) From the figure given with the question, let us first .consider the forward motion of the arm PQ from x = 0 to x = 2b. Obviously now the magnetic flux linked with the circuit SPQR is \[{{\phi }_{B}}=B.A.\] Hence, (a) \[{{\phi }_{B}}=BIx\] for \[0\le x\le b\] (b) \[{{\phi }_{B}}=0\] for \[b\le x\le 2b\] Consequently the induced emf will be e \[=\frac{-d{{\phi }_{B}}}{dt}.\] Hence, (a) \[e=-\frac{d}{dt}(BIx)=-BIx\] for \[0\le x\le b\] and (b) e = 0 for \[b\le x\le 2b\] Again for the backward motion of the arm PQ from x = 2b to x = 0, the magnetic flux linked with the circuit SPQR is (a) \[{{\phi }_{B}}=0\] for \[b\le x\le 2b\] and (b) \[{{\phi }_{B}}=BIx\] for \[0\le x\le b\] (and flux is gradually decreasing) As a result the induced emf will be (a) e = 0 for \[b\le x\le 2b,\] and (b) e = + Blv for \[0\le x\le b\] Variation of magnetic flux and indeced emf during forward and backward motion of the arm PQ is shown in figure given below. 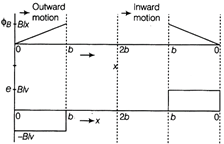
You need to login to perform this action.
You will be redirected in
3 sec
