| Light consisting of two wavelengths 400 nm and 560 nm is incident normally on Young's double slit of separation 0.1 mm. An interference pattern is formed on the screen placed 1.0 m from the slits. Calculate the separation between successive regions of total darkness. |
| Or |
| Find an expression for the linear width of central maxima in diffraction pattern obtained from a single slit. Also, draw a graph of intensity distribution pattern on the screen. |
Answer:
The location of nth minimum on the screen is given by \[x=\left( n-\frac{1}{2} \right)\frac{\Delta \lambda }{a}\] Let nth minimum of wavelength \[{{\lambda }_{1}}=400\,nm\]coincides with mth minimum of wavelength \[{{\lambda }_{2}}=560\,nm\] Then \[\left( n-\frac{1}{2} \right){{\lambda }_{1}}=\left( m-\frac{1}{2} \right){{\lambda }_{2}}\] \[\left( n-\frac{1}{2} \right)400\,nm=\left( m-\frac{1}{2} \right)560\,nm\] \[\frac{n-1/2}{m-1/2}=\frac{560}{400}=\frac{7}{5}\] or \[n=(7m-1)/5\] The possible integral values satisying this relation are \[{{n}_{1}}=4,\] \[{{m}_{1}}=3,\] \[{{n}_{2}}=11,\] \[{{m}_{2}}=8\] and so on. That is, \[{{4}^{th}}\]minimum of \[{{\lambda }_{1}}=400\,nm\] coincides with \[{{3}^{rd}}\] minimum of \[{{\lambda }_{2}}=560\,nm.\] The location of this minimum is \[{{x}_{1}}=\left( {{n}_{1}}-\frac{1}{2} \right)\frac{D{{\lambda }_{1}}}{d}\] where \[{{n}_{1}}=4\] Again, \[{{11}^{th}}\] minimum of \[{{\lambda }_{1}}=400\,nm\] coincides with \[{{3}^{rd}}\] minimum of \[{{\lambda }_{2}}=560\,nm.\] The location of this minimum is \[{{x}_{1}}=\left( {{n}_{1}}-\frac{1}{2} \right)\frac{D{{\lambda }_{1}}}{d}\] Again, \[{{11}^{th}}\] minimum of\[~{{\lambda }_{1}}=400\,nm\] coincides with \[{{8}^{th}}\] minimum of \[{{\lambda }_{2}}=560\,nm.\] The location of this minimum is \[{{x}_{2}}=\left( {{n}_{2}}-\frac{1}{2} \right)\frac{D{{\lambda }_{1}}}{d}\] Separation between successive regions of total darkness is \[{{x}_{2}}-{{x}_{1}}=\left( {{n}_{2}}-\frac{1}{2} \right)\frac{D{{\lambda }_{1}}}{d}-\left( {{n}_{1}}-\frac{1}{2} \right)\frac{D{{\lambda }_{1}}}{d}\] \[=\frac{D{{\lambda }_{1}}}{d}({{n}_{2}}-{{n}_{1}})\] \[=\frac{(1.0\,m)(400\times {{10}^{-9}}m)}{0.1\times {{10}^{-3}}m}(11-4)\] \[=28\times {{10}^{-3}}m=28\,mm\] Or Diffraction at a single slit Consider a narrow slit AB of width a. It is illuminated by monochromatic light of wavelength \[\lambda .\] A diffraction fringe pattern is obtained on a screen separated by a distance D. 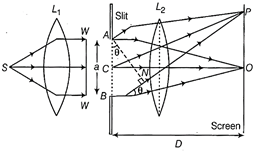 Diffraction at a single slit The slit AB is divided into two equal parts. For first secondary minima, Path difference (BN) \[=a\sin {{\theta }_{1}}=\lambda \] or \[\sin {{\theta }_{1}}=\lambda /a\] For second secondary minima, \[a\sin {{\theta }_{2}}=2\lambda \] or \[\sin {{\theta }_{2}}=2\lambda /a\] For nth secondary minima, \[a\sin {{\theta }_{n}}=n\lambda \] or \[\sin {{\theta }_{n}}=\frac{n\lambda }{a}\] Linear width of central maxima Angular width of central maxima is given by
Diffraction at a single slit The slit AB is divided into two equal parts. For first secondary minima, Path difference (BN) \[=a\sin {{\theta }_{1}}=\lambda \] or \[\sin {{\theta }_{1}}=\lambda /a\] For second secondary minima, \[a\sin {{\theta }_{2}}=2\lambda \] or \[\sin {{\theta }_{2}}=2\lambda /a\] For nth secondary minima, \[a\sin {{\theta }_{n}}=n\lambda \] or \[\sin {{\theta }_{n}}=\frac{n\lambda }{a}\] Linear width of central maxima Angular width of central maxima is given by 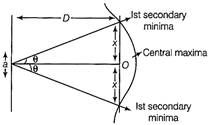 Angular width of central maxima \[\sin \theta =\frac{2\lambda }{a}\] But \[\tan \theta =\frac{x}{D}\] For small angle \[\theta ,\] \[\sin \theta \approx \tan \theta \] \[\therefore \] \[\frac{2\lambda }{a}=\frac{x}{D}\] or \[x=\frac{2D\lambda }{a}\] Intensity distribution pattern is shown below
Angular width of central maxima \[\sin \theta =\frac{2\lambda }{a}\] But \[\tan \theta =\frac{x}{D}\] For small angle \[\theta ,\] \[\sin \theta \approx \tan \theta \] \[\therefore \] \[\frac{2\lambda }{a}=\frac{x}{D}\] or \[x=\frac{2D\lambda }{a}\] Intensity distribution pattern is shown below 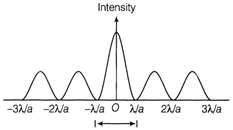 Variation of intensity with angle \[\theta \] in single slit diffraction
Variation of intensity with angle \[\theta \] in single slit diffraction
You need to login to perform this action.
You will be redirected in
3 sec
