question_answer

A massive platform of mass M is moving with speed \[v=6m{{s}^{-1}}\]. At. \[t=0,\] a body of mass \[m(m<<M)\] is gently placed on the platform. If coefficient of friction between the body and platform is \[\mu =0.3\] and \[g=10\,\,m/{{s}^{2}}\]. Then,

A) the body covers a distance 3 m on the platform in the direction of motion of the platform

B) the body covers a distance 3 m on the platform opposite to the direction of motion of platform before coming to rest

C) the body covers a distance 6 m on the platform in the direction of motion of the platform

D) the body covers a distance 6 m on the platform opposite to the direction of motion of platform before coming to rest

Correct Answer: D

Solution :

Idea The kinetic friction will act only if there is a relative motion between the two surfaces. In this question the relative motion between them will stop when their velocities become same and in this situation the force of friction between them will become zero.

Since, M >> m, the velocity of M remains unchanged after m is placed on to it. Acceleration   of m is a \[a=\frac{\mu mg}{m}=mg\]

Initial relative acceleration

\[{{a}_{mM}}={{a}_{mE}}-{{a}_{mE}}=a-0=a\]

and initial relative velocity,

\[{{v}_{mM}}={{v}_{mE}}+{{v}_{mE}}=0-v=-v\]

Hence, \[{{S}_{mM}}=\frac{{{v}^{2}}}{2\mu g}=\frac{{{(6)}^{2}}}{2\times 0.3\times 10}=6\]m

TEST Edge

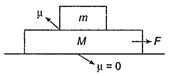In the above case the force acting on the above block is only friction,

\[\Rightarrow \] So \[{{a}_{\max }}\] for the upper block = \[\frac{\mu mg}{m}=\mu g\]

\[\Rightarrow \]So if the maximum acceleration of lower block is\[\mu g\]then only they both could move together otherwise kinetic friction will act.