question_answer

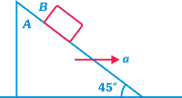
If the coefficient of friction between A and B is \[{{m}_{2}}\], the maximum horizontal acceleration of the wedge A for which B will remain at rest with respect to the wedge is:

A) \[{{m}_{1}}={{m}_{2}}\]                               

B) \[{{m}_{2}}\]

C) \[{{m}_{1}}={{m}_{2}}\]                               

D) \[{{m}_{2}}\]

Correct Answer: B

Solution :

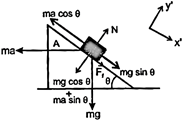
FBD of block B w.r.t. wedge A, for maximum 'a' perpendicular to wedge:

\[\sum {{f}_{y'}}=\left( mg\cos \theta +ma\sin \theta -N \right)=0\] and

\[\sum {{f}_{x'}}=mg\sin \theta +\mu N-ma\cos \theta =0\]

(for maximum a)

\[T'=2\sec \] \[mg\sin \theta +\mu \left( mg\,\cos \theta +ma\sin \theta  \right)-ma\cos \theta =0\]\[\Rightarrow a=\frac{\left( g\,\sin \theta +\mu g\cos \theta  \right)}{\cos \,\theta -\mu \sin \,\theta }\]

for \[\frac{{{T}_{1}}}{{{T}_{2}}}=\sqrt{\frac{g+\frac{g}{4}}{g}}=\frac{\sqrt{5}}{2}\]

\[\Rightarrow a=g\left( \frac{\tan \,45{}^\circ +\mu }{\cot \,45{}^\circ -\mu } \right)\,;\,\,a=g\left( \frac{1+\mu }{1-\mu } \right)\]