| A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downward as in figure and whose equation is\[{{x}^{2}}=ay\]. If the coefficient of friction is \[{{M}_{1}}\] the highest distance above the x-axis at which the particle will be in equilibrium is |
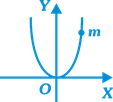 |
A) \[\mu a\]
B) \[{{\mu }^{2}}a\]
C) \[\frac{1}{4}{{\mu }^{2}}a\]
D) \[\frac{1}{2}\mu a\]
Correct Answer: C
Solution :
| For the sliding not to occur when\[=\frac{1}{2}\left( \frac{4M}{3} \right){{R}^{2}}-\left[ \frac{1}{2}\left( \frac{M}{3} \right){{\left( \frac{R}{2} \right)}^{2}}+{{\left( \frac{R}{2} \right)}^{2}} \right]=\frac{13}{24}\,M{{R}^{2}}\] |
| \[\tan \theta =\frac{dy}{dx}=\frac{2x}{a}=\frac{2\sqrt{ay}}{a}=2\sqrt{\frac{y}{a}}\] |
| \[\therefore \,\,\,2\sqrt{\frac{y}{a}}\le \mu \] or \[y\le \frac{a{{\mu }^{2}}}{4}\] |
You need to login to perform this action.
You will be redirected in
3 sec
