| Two blocks are placed on a wedge with coefficients of friction being different for two blocks. Choose the correct option (friction is not sufficient to prevent the motion). |
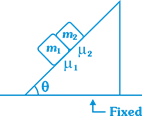 |
A) if\[{{m}_{1}}<{{m}_{2}}\], then normal reaction between blocks will be non-zero
B) if\[{{m}_{1}}={{m}_{2}}\]then normal reaction between the blocks will be zero
C) if\[{{\mu }_{1}}={{\mu }_{2}}\], then normal reaction between the blocks will be zero
D) None of the above
Correct Answer: C
Solution :
| Idea The normal reaction between the blocks will be non-zero only if the initial acceleration of block \[{{m}_{2}}\] is more than block \[{{m}_{1}}\]. Then, only the block \[{{m}_{2}}\] will push block \[{{m}_{1}}\] and normal reaction will develop and it is possible only when \[{{\mu }_{2}}<{{\mu }_{1}}\] |
| The normal reaction between the blocks will not depend on the masses \[{{m}_{1}}\]and\[{{m}_{2}}\]. |
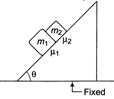 |
| If \[{{\mu }_{1}}={{\mu }_{2}}=\mu \] |
| \[\Rightarrow \] \[{{a}_{1}}=(g\sin \theta -\mu g\cos \theta )\] |
| \[\Rightarrow \]\[{{a}_{2}}=(g\sin \theta -\mu g\cos \theta )\] |
| \[\Rightarrow \]\[{{a}_{1}}={{a}_{2}}\] |
| So, there is no relative motion between the blocks, so normal reaction between them is zero. |
| TEST Edge Both are identical planes, if m does not slip then M will? |
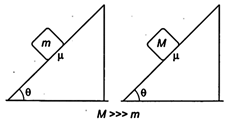 |
| M will also not slip because in this case motion of block will depend only on (l not on mass of the block. |
You need to login to perform this action.
You will be redirected in
3 sec
