question_answer

An insect crawls up on a hemispherical surface very slowly (figure). The coefficient of friction between the insect and the surface is \[1/3\]. If the line joining the centre of hemispherical surface of the insect makes an angle a with the vertical, the maximum possible value of a is given by                         

A) cot\[\alpha \] = 3    

B) tan\[\alpha \]= 3

C) sec\[\alpha \]= 3           

D) cosec\[\alpha \]= 3

Correct Answer: A

Solution :

      

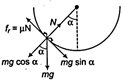
Idea Angle will be maximum, when insect will crawl upto a certain height at which maximum static friction on insect will be counter balanced by its tangential component of its weight.

To avoid slipping, \[{{f}_{r}}=mg\,\sin \,\,\alpha \] at maximum\[\alpha \]

\[\mu N=mg\sin \alpha \]

\[\Rightarrow \]\[\mu \,mg\cos \alpha =mg\sin \alpha \]

\[\therefore \,\,\mu \,\,=\,\,\tan \,\alpha \]

\[\Rightarrow \]\[\tan \alpha =\frac{1}{3}\] \[\left( \text{as,}\mu \,\text{=}\frac{1}{3} \right)\]

\[\therefore \]\[\cot \alpha =3\]